Operations On Whole Numbers

Operations on whole numbers are discussed here:

The four basic operations on whole numbers are addition; subtraction; multiplication and division. We will learn about the basic operations in more detailed explanations along with the examples. 

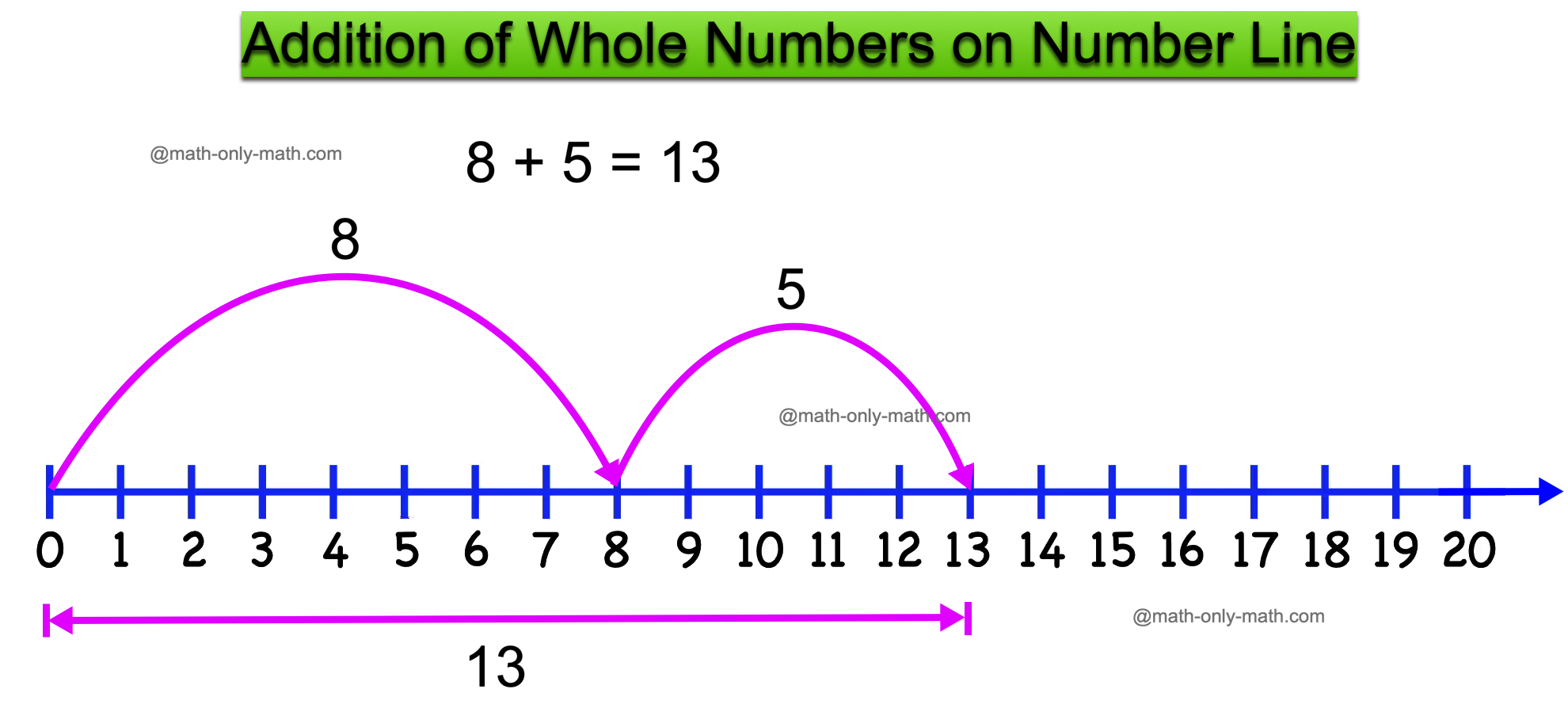
I. Addition of Whole Numbers:

Addition is the process of adding two or more numbers as one sum, represented by the symbol '+'. The numbers added are called addends and the result of addition is called the sum.

Addition can be performed on a number line.

For example:

Properties of Addition of Whole Numbers:

1. Closure Property: The sum of two whole numbers is also a whole number. If a and b are any two whole numbers, then a + b is also a whole number.

For example:

7 + 3 = 10;

6 + 6 = 12;

8 + 9 = 17;

5 + 8 = 13.

2. Commutative Property: In whatever order we add two whole numbers, the sum remains the same. If a and b are any two whole numbers, then a + b = b + a.

For example:

(i) 7 + 8 = 15 and 8 + 7 = 15.

(ii) 6 + 7 = 13 and 7 + 6 = 13.

3. Associative Property: If a, b and care any three whole numbers, then (a + b) + c = a + (b + c). This is also equal to (a + c) + b.

The numbers can be associated (kept together) in any order for the addition.

For example:

(i) (35 + 25) + 40 = 60 + 40 = 100

(ii) 35 + (25 + 40) = 35 + 65 = 100

(iii) (35 + 40) + 25 = 75 + 25 = 100

This property helps us in deciding which two numbers to be added first so that calculation become easier. While adding three or more numbers, we group them. We need not ad them in the order, the numbers are given. We arrange them suitably and add.

4. Additive Identity: If a is any whole number, then: a + 0 = 0 + a = a .

For example:

3 + 0 = 0 + 3 = 3;

8 + 0 = 0 + 8 = 8;

9 + 0 = 0 + 9 = 9.

Here, the number 0 is called the identity element for addition. It is also called the additive identity.

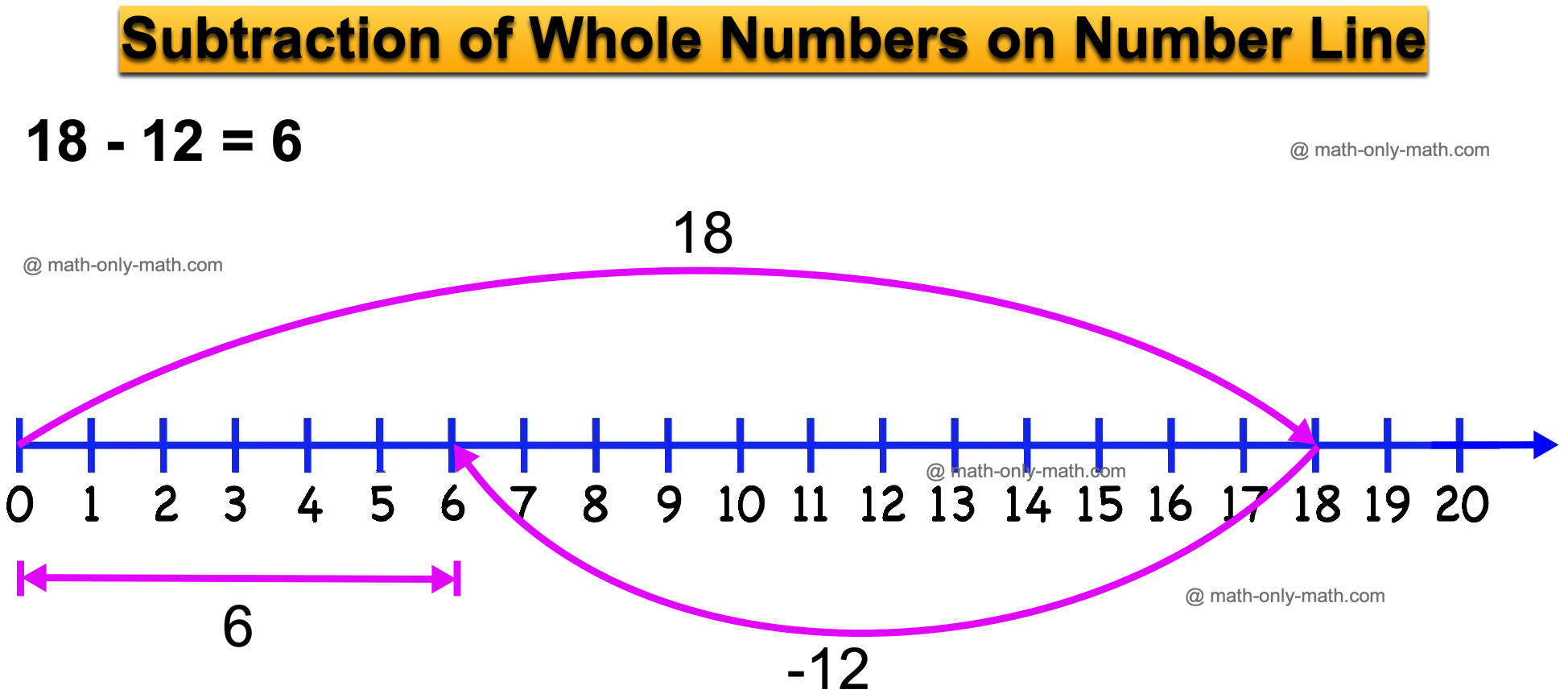
II. Subtraction of Whole Numbers:

Subtraction is the process of finding difference between two numbers or quantities. It is the inverse process of addition. In subtraction, the number from which another number is subtracted is called the minuend, and the number which is subtracted is called the subtrahend. The resu is called the difference.

Subtraction can be performed on a number line.

For example: 

Properties of Subtraction of Whole Numbers:

1. Closure Property: If a and b are any two whole numbers, then a - b is not always a whole number. Only when a > b or a = b then a - b will be a whole number.

For example:

(1) 17 - 6 = 11, which is a whole number because 17 > 6

(ii) 8 - 8 = 0, which is a whole number because 8 = 8.

(iii) 3 - 9 is not a whole number because 3 < 9

Thus, we may conclude that the closure property does not hold good for subtraction of whole numbers.

2. Commutative Property: If a and b are two distinct whole numbers, then a - b is not equal to b - a i.e., the operation of subtraction is not commutative.

For example:

8 - 3 = 5, which is a whole number.

But, 3 - 8 does not give a whole number.

So, 8 - 3 ≠ 3 - 8.

3. Associative Property: If a, b and c are any three whole numbers, (a - b) - c ≠ a - (b - c), i.e., the operation of subtraction is not associative.

For example:

(8 - 3) - 2 = 5 - 2 = 3 and = 8 - (3 - 2) = 8 - 1 = 7

So, (8 - 3) - 2 ≠ 8 - (3 - 2)

4. Zero Property: If a is any whole number, a - 0 = a (a whole number), whereas 0 - a is not whole number. Only when a is equal to zero, we get 0 - 0 = 0.

If we subtract 0 from a whole number, the result is the number itself.

For example:

7 - 0 = 7, which is a whole number. 0 - 7 does not give a whole number.

Thus, we can say that if a non-zero whole number is subtracted from zero, the result is not a whole number.

5. Identity Property: When a whole number is subtracted from itself, the result is always zero. 

For example:

(i) 5 - 5 = 0

(ii) 7 - 7 = 0

6. Property: If a, b and c are three whole numbers, then a - b = c ⟹ b + c = a.

For example:

(i) 21 - 8 = 13 ⟹ 13 + 8 = 21

(ii) 17 - 5 = 12 ⟹ 12 + 5 = 17

The operations of addition and subtraction are inverse of each other.

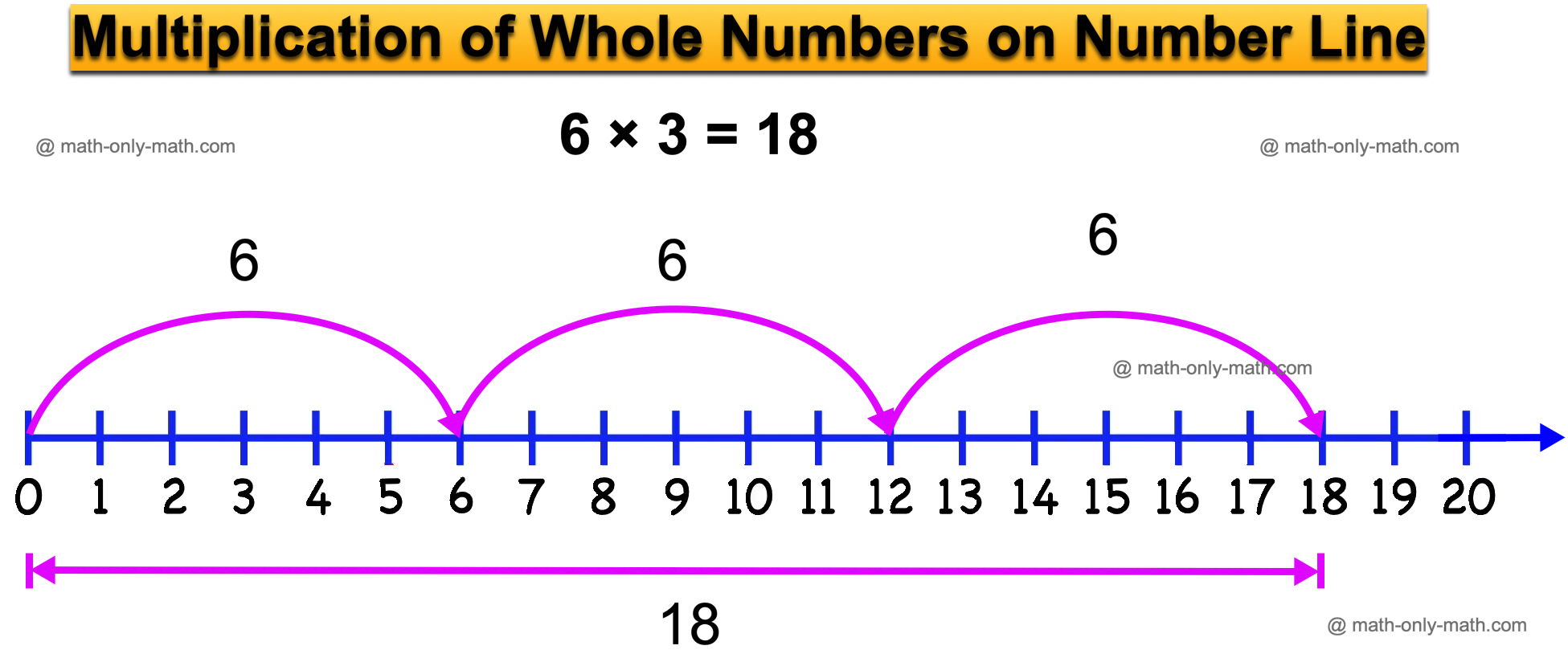
III. Multiplication of Whole Numbers:

In multiplication, the number which is multiplied is called the multiplicand and the number by which another number is multiplied is called the multiplier. The result is called the product.

As multiplication is the repeated addition, the multiplication of whole number can be shown on a number line.

For example:

Properties of Multiplication of Whole Numbers:

1. Closure Property: The product of two whole numbers is always a whole number. If a and b are any two whole numbers, then ab is always a whole number.

This is called the closure property of multiplication.

For example:

6 × 7 = 42, which is a whole number.

7 × 9 = 63, which is a whole number.

9 × 8 = 72, which is a whole number.

2. Commutative Property: The product of any two whole numbers remains the same, even if we change their orders. If a and b are any two whole numbers, then a × b = b × a.

This is called the commutative property of multiplication.

For example:

(i) 4 × 8 = 8 × 4 = 32

(ii) 6 × 9 = 9 × 6 = 54

3. Associative Property: If a, b and care any three whole numbers, then (a × b) × c = a × (b × c).

This is called the associative property or law of multiplication.

For example:

We can multiply 12 × 24 × 5 in the following ways:

(i) (12 × 24) × 5 = 288 × 5 = 1440

(ii) 12 × (24 × 5) = 12 × 120 = 1440

(iii) (12 × 5) × 24 = 60 × 24 = 1440

The answer is the same in all cases. Thus, we conclude that for multiplying whole numbers, we may change the arrangements, but the product remains the same.

4. Multiplicative Property of 0:

The product of any whole number and zero is always zero. If a is any whole number, then a × 0 = 0 × a = 0. This is called the multiplicative property of 0.

For example:

(i) 3 × 0 = 0 = 0 × 3

(ii) 7 × 0 = 0 = 0 × 7

5. Multiplicative Property of 1:

If a is any whole number, then 1 × a = a × 1 = a.

This is called the multiplicative property of 1. 

For example:

(i) 5 × 1 = 1 × 5 = 5

(ii) 4 × 1 = 1 × 4 = 4

(iii) 15 × 1 = 1 × 15 = 15

From the above, we observe that the result obtained by multiplying a whole number by 1 is the number itself. Here, 1 is called the identity element with respect to multiplication. It is also called the multiplicative identity.

6. Distributive Property of Multiplication Over Addition: If a, b and c are any three whole numbers, then a(b + c) = a × b + a × c.

This is called the distributive property of multiplication over addition.

For example:

(i) 12 × (8 + 6) = 12 × 14 = 168 and 12 × 8 + 12 × 6 = 96 + 72 = 168

Thus, 12 × (8 + 6) = 12 × 8 + 12 × 6.

(ii) 24 × (4 + 7) = 24 × 11 = 264 and 24 × 4 + 24 × 7 = 96 + 168 = 264.

Thus, 24 × (4 + 7) = 24 × 4 + 24 × 7.

7. Distributive Property of Multiplication Over Subtraction: If a, b and c are any three whole numbers, then a × (b - c) = a × b - a × c.

This is called distributive property of multiplication over subtraction. 

For example:

(i) 15 × (7 - 5) = 15 × 2 = 30 and 15 × 7 - 15 × 5 = 105 - 75 = 30.

Thus, 15 × (7 - 5) = 15 × 7 - 15 × 5.

(ii) 20 × (15 - 5) = 20 × 10 = 200 and 20 × 15 - 20 × 5 = 300 - 100 = 200.

Thus, 20 × (15 - 5) = 20 × 15 - 20 × 5.

7. Property: If a, b and c are any three whole numbers such that a > b and c is a non-zero whole number, then a × c > b × c.

For example:

Let us take three whole numbers 24, 8 and 12.

Here, 24 > 8 and 12 is a non-zero number.

By multiplying 24 and 8 by 15, we get:

24 × 15 = 360 and 8 × 15 = 120

Clearly, 360 > 120.

IV. Division of Whole Numbers:

In a division, the number which is to be divided is called the dividend, the number by which another number is divided is called divisor, the result is called the quotient, and the number which is left is called the remainder.

Thus: Dividend = Divisor × Quotient + Remainder

Properties of Division of Whole Numbers:

1. Closure Property: If a and b are any two whale numbers where b = 0 then a + b is not necessarily a whole number.

For example:

(i) 36 ÷ 9 = 4, which is a whole number

(ii) 3 ÷ 8 = \(\frac{3}{8}\), which is not a whole number.

Whole numbers are not closed under division.

2. Division by Zero (0) Property: Division of any whole number by 0 is not defined.

For example:

Let us try to divide 18 by 0. This is equal to finding a whole number which when multiplied by 0 gives 18. This is absurd, because no whole number which when multiplied by 0 will give us 18.

3. Division by One (1) Property: If a is any whole number, then a ÷ 1 = a.

For example:

(i) 8 ÷ 1 = 8

(ii) 14 ÷ 1 = 14 and

(iii) 57 ÷ 1 = 57

When we divide any whole number by 1, the result is the number itself.

4. Division by Itself: If a is any whole number other than zero, then a ÷ a = 1.

For example:

(i) 9 ÷ 9 = 1;

(ii) 15 ÷ 15 = 1 and

(iii) 63 ÷ 63 = 1

5. Zero Division Property: If a is any whole number other than zero, then 0 ÷ a = 0.

For example:

(i) 0 ÷ 8 = 0

(ii) 0 ÷ 16 = 0

but a ÷ 0 is not defined.

Worked-out Problems Related to Operations on Whole Numbers:

1. Solve using rearrangement: 

(a) 784 + 127 + 216

Solution: 

784 + 127 + 216

= (784 + 216) + 127

= 1000 + 127 

= 1127 

(b) 25 × 8 × 125 × 4 

Solution: 

25 × 8 × 125 × 4 

= (125 × 8) × (25 × 4) 

= 1000 × 100 

= 100000

2. Find the value using distributive property. 

(a) 2651 × 62 + 2651 × 38 

Solution: 

2651 × 62 + 2651 × 38 

Property: a × b + a × c = a × (b + c) 

= 2651 × (62 + 38) 

= 2651 × 100 

= 265100 

(b) 347 × 163 - 347 × 63 

Solution: 

347 × 163 - 347 × 63 

Property: a × b - a × c = a × (b - c) 

= 347 × (163 - 63) 

= 347 × 100 

= 34700 

(c) 128 × 99 + 128 

Solution: 

128 × 99 + 128 

Property: a × b - a × c = a × (b + c) 

= 128 × 99 + 128 

= 128 × (99 + 1) 

= 12800 

3. Find the product using distributive property: 

(a) 237 × 103 

Solution: 

237 × 103 

237 × (100 + 3) 

Property: a × (b + c) = a × b + a × c 

Therefore, 237 × (100 + 3) 

= 237 × 100 + 237 × 3 

= 23700 + 711

= 24411 

(b) 510 × 99 

Solution:

510 × 99

510 × (100 - 1)

Property: a × (b - c) = a × b - a × c

Therefore, 510 × (100 - 1)

= 510 × 100 - 510 × 1

= 51000 - 510

= 50490

4. Verify the following:

(a) 537 + 265 = 265 + 537

Solution:

537 + 265 =265 + 537

L.H.S. = 537 + 265 = 802

R.H.S. = 265 + 537 = 802

Property: a + b =b + a

Therefore, L.H.S. = R.H.S.

Hence, verified.

(b) 25 × (36 × 50) = (25 × 36) × 50

Solution:

25 × (36 × 50) = (25 × 36) × 50

L.H.S.= 25 × (36 × 50) = 25 × 1800 = 45000

R.H.S. = (25 × 36) × 50 = 900 × 50 = 45000

Property: a × (a × c) = (a × b) × c

Therefore, L.H.S. = R.H.S.

Hence, verified.

5. Find the least number that must be subtracted from 1000 so that 45 divides the difference exactly.

Solution:

Divide 1000 by 45.

Now 1000 - 10 = 990

Therefore, 10 should be subtracted from 1000 so that difference 990 is divisible by 45.

6. Find the least number that should be added to 1000 so that 65 divides the sum exactly.

Solution:

Divide 1000 by 65.

Now finding the difference between the divisor and remainder, we get

65 - 25 = 40

Therefore, 40 must be added to 1000 so that the sum 1040 is exactly divisible by 65.

7. Find the number which when divided by 15 gives 7 as the quotient and 3 as the remainder.

Solution:

Dividend = divisor × quotient + remainder

= 15 × 7 + 3

= 105 + 3 = 108

Therefore, the required number is 108

● Operations On Whole Numbers

● Addition Of Whole Numbers.

● Subtraction Of Whole Numbers.

● Multiplication Of Whole Numbers.

● Properties Of Multiplication.

● Division Of Whole Numbers.

● Properties Of Division.

5th Grade Math Problems 

From Operations On Whole Numbers to HOME PAGE

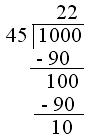
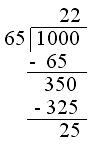
New! Comments

Have your say about what you just read! Leave me a comment in the box below. Ask a Question or Answer a Question.

Share this page: What’s this?

FacebookXPinterestWhatsAppReddit

ShareFacebookXPinterestWhatsAppReddit