Concept of Parabola

We will discuss about the basic concept of parabola and its definition.

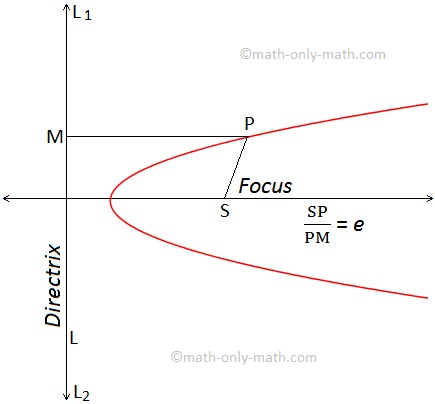
Definition of Parabola: A parabola is the locus of a fixed point which moves on a plane such a way that its distance from a fixed point in the plane is always equidistant from the fixed point and the fixed straight line.

Let S be a fixed point and L, a fixed straight line which is not passing through S on a plane.

If a point P moves on this plane in such a way that it is always equidistant from the fixed point S and the fixed straight line L then the locus of the point P is called a Parabola.

Then by definition

SP = PM

Where PM is the length of the perpendicular from P on the directrix ZZ'.

 

What is the directrix of the parabola?

The fixed point S is called the focus and the fixed straight line L is called is called the directrix of the parabola.

 

What is the axis of the parabola?

The straight line through the focus and perpendicular to the directrix is called the Axis of the parabola.

 

What is the vertex of the parabola?

The point at which the axis intersects the parabola is called the vertex of the parabola.

or,

The point on the axis midway between the focus and directrix is called the vertex of the parabola.

 

What is the focal chord of the parabola?

A chord passing through its focus is called a Focal chord of the parabola.

 

What is the double ordinate of the parabola?

Any chord perpendicular to the axis of the parabola is called its double ordinate.

What is the latus rectum of the parabola?

The double ordinate through the focus of a parabola is called its latus rectum.

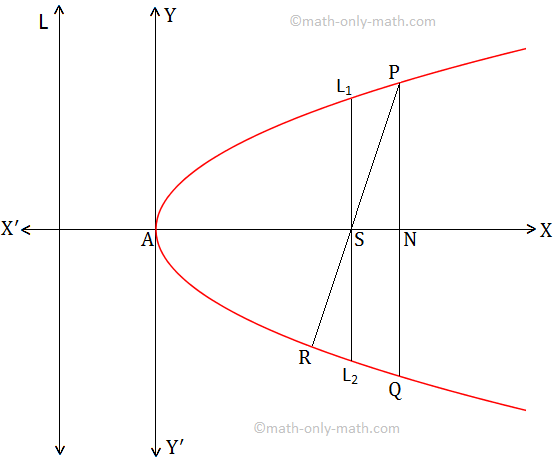
In the adjoining figure

(i) the point S represents the focus

(ii) the point A represents the vertex

(iii) the straight line L represents the directrix

(iv) the straight line AS represents the axis

(v) PN represents the ordinate of a point P on the parabola

(vi) PNQ represents the double ordinate of P

(vii) AN represents the abscissa of P

(viii) L\(_{1}\)L\(_{2}\) represents the latus rectum.

(ix) PSR represents the focal chord of the parabola.

Solved example on the basic concept of parabola:

Find the equation of the parabola whose directrix is x + 5 = 0 and focus (-3, 0).

Solution:

Let P(x, y) be any point on the parabola having directrix as the line x + 5 = 0 and focus at S(-3, 0).

Therefore, SP = PM, where PM is the length of the perpendicular from P on the directrix

⇒ SP\(^{2}\) = PM\(^{2}\)

⇒ (x + 3)\(^{2}\) + (y – 0)\(^{2}\) = \((\mathrm{\frac{x + 0y + 5}{\sqrt{1 + 0}}})^{2}\)

⇒ x\(^{2}\) + 6x + 9 + y\(^{2}\) = (x + 5)\(^{2}\)

⇒ x\(^{2}\) + 6x + 9 + y\(^{2}\) = x\(^{2}\) + 10x + 25

⇒ y\(^{2}\) = 4x + 16, which is the required equation of the parabola.

● The Parabola

• Concept of Parabola
• Standard Equation of a Parabola
• Standard form of Parabola y22 = - 4ax
• Standard form of Parabola x22 = 4ay
• Standard form of Parabola x22 = -4ay
• Parabola whose Vertex at a given Point and Axis is Parallel to x-axis
• Parabola whose Vertex at a given Point and Axis is Parallel to y-axis
• Position of a Point with respect to a Parabola
  
• Parametric Equations of a Parabola
• Parabola Formulae
• Problems on Parabola

11 and 12 Grade Math 

From Concept of Parabola to HOME PAGE