Subscribe to our YouTube channel for the latest videos, updates, and tips.
Home | About Us | Contact Us | Privacy | Math Blog
Calculate Simple Interest
How to calculate simple interest?
Principal: The money which we deposit in or the lower from the bank or the money learned called the principal.
Rate of interest: The interest paid on $ 100 for one year is called the rate per cent per year or rate per cent per annum.
Time: The period of time for which the money is lent or invested.
Interest: Additional money paid by the borrowed to the lender for using the money is called interest.
Simple Interest: If the interest is calculated uniformly on the original principal throughout the lone period, it is called simple interest.
Amount: The total money paid back to the lender is called the amount.
Calculate Simple Interest
Formula to calculate Simple Interest?
If P denotes the principal ($), R denotes the rate (percentage p.a.) and T denotes time (years), then:-
S.I = (P × R × T)/100
R = (S.I × 100)/(P × T)
P = (S.I × 100)/(R × T)
T = (S.I × 100)/(P × R)
If the denotes the amount, then A = P + S.I
Note:
● When we calculated the time period between two dates, we do not could the day on which money is deposited but we count the day on which money is retuned.
● Time is always taken according to the per cent rat.
● For converting time in days into years, divide th number of days by 365 (for ordering or lap year.)
● For converting time in month into years, divide th number of month by 12 (for ordering or lap year.)
Examples to find or calculate simple interest when principal, rate and time are known
Calculate Simple Interest
Find the simple interest on:
(a) $ 900 for 3 years 4 months at 5% per annum. Find the amount also.
Solution:
P = $ 900,
R = 5% p.a.
T = 3 years 4 months = 40/12 years = 10/3 years
Therefore, S.I = (P × R × T)/100 = (900 × 5 × 10)/(100 × 3) = $ 150
Amount = P + S.I = $ 900 + $ 150 = $ 1050
(b) $ 1000 for 6 months at 4% per annum. Find the amount also.
Solution:
P = $ 1000,
R = 4% p.a.
T = 6 months = 6/12 years
S.I = (P × R × T)/100 = (1000 × 4 × 1)/(100 × 2) = $ 20
Therefore, A = P + I = $( 1000 + 20) = $ 1020
(c) $ 5000 for 146 days at 15¹/₂% per annum.
Solution:
P = $ 5000,
R = 151/2% p.a.
T = 146 days
S.I = ( 5000 × 31 × 146)/(100 × 2 × 365)
= $ 10 × 31 = $ 310
(d) $ 1200 from 9ᵗʰ April to 21ˢᵗ June at 10% per annum.
Solution:
P = $ 1200,
R = 10% p.a.
T = 9th April to 21st June
= 73 days [April = 21, May = 31, Jun = 21, 73 days]
= 73/365 years
S.I = (1200 × 10 × 73)/(100 × 365) = $ 24
Examples to find or calculate Time when Principal, S.I and Rate are known
Calculate Simple Interest
1. In how much time dose $ 500 invested at the rate of 8% p.a. simple interest amounts to $ 580.
Solution:
Here P = $ 500, R = 8% p.a A = $ 580
Therefore S.I = A - P = $ (580 - 500) = $ 80
Therefore T = (100 × S.I)/(P × R) = (100 × 80)/(500 × 3) = 2 years
2. In how many years will a sum of $ 400 yield an interest of $ 132 at 11% per annum?
Solution:
P = $ 400,
R = 11%
S.I = $ 132
T = (100 × S.I)/(P × R) = (132 × 100)/(400 × 11) = 3 years
Calculate Simple Interest
3. In how many years will a sum double itself at 8 % per annum?
Solution:
Let Principal = P, then, Amount = 2P
So , S.I. = A - P = 2P – P = P
T = (100 × S.I)/(P × R) = ( 100 × P)/(P × 8) = 25/2 = 121/2 years
Calculate Simple Interest
4. In how many years will simple interest on certain sum of money at 6 1/4% Per annum be 5/8 of itself?
Solution:
Let P = $ x, then S.I = $ 5/8 x
Rate = 6 1/4% = 25/4 %
Therefore T = ( 100 × S.I)/(P × R) = ( 100 × 5/8)/(x × 25/4) x = ( 100 × 5 × x × 4)/(x × 8 × 25)
T = 10 years
Examples to find or calculate Rate per cent when Principal, S.I. and Time are known
1. Find at what rate of interest per annum will $ 600 amount to $ 708 in 3 years.
Solution:
P= $ 600 , A = $ 708 Time = 3 years
Therefore S.I. = $ 708 - $ 600 = $ Rs. 108
Now, R = ( 100 × S.I)/(P × R) = (100 × 108)/(600 × 3) = 6% p.a.
Calculate Simple Interest
2. Simple interest on a certain sum is 36/25 of the sum. Find the Rate per cent and time if they are both numerically equal.
Solution:
Let the Principal be $ X Then S.I. = 36/25 x
R = ? T = ?
Let Rate = R % per annum, then Time = R years.
So S.I. = (P × R × T)/100 → 36/25 x = (x × R × T)/100
--- ( 36 × 10 × x)/(25 × x) = R2
----- R2 = 36 × 4 ----- R = √(36 × 4) = 6 × 2
Therefore Rate = 12 % p.a. and T = 12 years
Calculate Simple Interest
3. At what rate per cent per annum will $ 6000 produce $ 300 as S.I. in 1 years?
Solution:
P= $ 600, T = 1 year S.I. = $ 300
Therefore R = ( S.I × 100)/(P × R) = ( 300 × 100)/(6000 × 1) = 5% p.a
4. At what rate per cent per annum will a sum triple itself in 12 years ?
Solution:
Let the sum be $ P, then Amount = $ 3P
S.I. = $ 3P – P = $ 2P, Time = 12 years
Now, R =( S.I × 100)/(P × R) = (100 × 2P)/(P × 12) = 50/3 = 16.6 %
Examples to find or calculate Principal when Rate, Time and S.I. are known
Calculate Simple Interest
1. What sum will yield $ 144 as S.I. in 21/2 years at 16% per annum?
Solution:
Let P = $ x, S.I. = $ 144
Time = 21/2 years or 5/2 years, Rate = 16%
So, P = ( 100 × S.I)/(P × R) = ( 100 × 144)/(16 × 5/2) = ( 100 × 144 × 2)/(16 × 5) = $ 360
2. A some amount to $ 2040 in 21/2 years at , P = ?
Solution:
Let the principal = $ x
S.I. = $ (x × 11 × 5/2 × 1/100) = $ 11x/40
Amount = P + S.I. = x/1 + 11x/40 = (40x × 11x)/40 = 51x/40
But 51x/40 = 2040
51x = 2040 × 40 ---- x = (2040 × 40)/51 = $ 1600
Calculate Simple Interest
3. A certain sum amounts to $ 6500in 2 years and to $ 8750 in 5 years at S.I. Find the sum and rate per cent per annum.
Solution:
S.I. for 3 years = Amount after 5 years – Amount after 2 years
= $ 8750 – $ 6500 = 2250
S.I. for 1 years = Rs. 2250/3 = $ 750
Therefore S.I. for 2 years = $ 500× 2 = $ 1500
So, sum = Amount after 2 years – S.I.for 2 years
= $ 6500- 1500 = $ 5000
Now, P = Rs.5000, S.I. = $ 1500, Time = 3 years
R = ( 100 × S.I)/(P × T) = (100 × 1500)/(5000 × 2) = 15%
Therefore The sum is $ 5000 and the rate of interest is 15%
4. Divide $ 6500 in to two parts , such that if one part is lent out at 9% per annum and other at 10% per annum, the total yearly income is $ 605
Solution:
Let the first part be $ x. Second part = $ (6500 - x )
Now S.I. on $ X at 9% per annum for 1 year = $ (x × 9 × 1)/100 = 9x/100
S.I. on $ (6500 – x ) at 10% per annum
1 year = $ ((6500-x) × 10 × 1)/100 = $ ((6500 - x))/10
Total S.I = $ (9x/100+ (6500 - x)/10) = ((9x + 6500 - 10x)/100)
= $ ( 65000 - x)/100
But given that total S.I.= $ 605
So, (6500 - x)/100 =605 -----65000 - x = 60500
----- 65000 – 60500 = x ---- x = $ 4500
Now, second part = 6500 – x = 6500 – 4500 = $ 2000
Hence, first part = $ 2000 and second part = $ 4500
5. When the rate of interest in a bank is increased from 9% to 10% per annum; A person deposits $ 500 more into his account. If the annual interest now Received by him is $ 150more then before, find his original deposit.
Solution:
Let the original deposits be $ x
Then, S.I. on $ x for 1 year at (10 - 9 )% = 1% per annum + S.I. on $ 500
For I year at 10% per annum = $ 15
----- ( x × 1 × 1)/100 + ( 500 × 10 × 1)/100 = 150
----- x/(100 ) + 50 = 150 ---- x/(100 ) + 150 – 50 ----- x/(100 ) + 100
----- x = 100 × 100 = $
10,000
Therefore, the original deposit is $ 10,000.
Calculate Simple Interest
● Simple Interest
Practice Test on Simple Interest
● Simple Interest - Worksheets
From Calculate Simple Interest to HOME PAGE
Didn't find what you were looking for? Or want to know more information about Math Only Math. Use this Google Search to find what you need.
Recent Articles
-
5th Grade Circle Worksheet | Free Worksheet with Answer |Practice Math
Jul 11, 25 02:14 PM
In 5th Grade Circle Worksheet you will get different types of questions on parts of a circle, relation between radius and diameter, interior of a circle, exterior of a circle and construction of circl… -
Construction of a Circle | Working Rules | Step-by-step Explanation |
Jul 09, 25 01:29 AM
Construction of a Circle when the length of its Radius is given. Working Rules | Step I: Open the compass such that its pointer be put on initial point (i.e. O) of ruler / scale and the pencil-end be… -
Combination of Addition and Subtraction | Mixed Addition & Subtraction
Jul 08, 25 02:32 PM
We will discuss here about the combination of addition and subtraction. The rules which can be used to solve the sums involving addition (+) and subtraction (-) together are: I: First add -
Addition & Subtraction Together |Combination of addition & subtraction
Jul 08, 25 02:23 PM
We will solve the different types of problems involving addition and subtraction together. To show the problem involving both addition and subtraction, we first group all the numbers with ‘+’ and… -
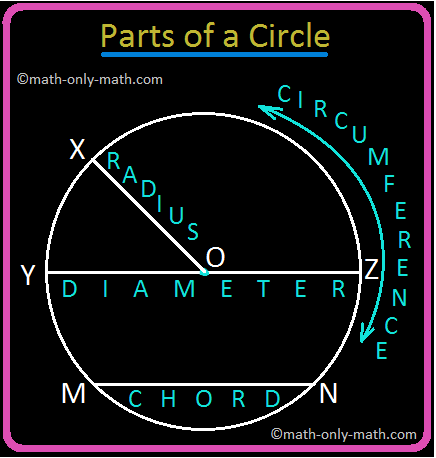
5th Grade Circle | Radius, Interior and Exterior of a Circle|Worksheet
Jul 08, 25 09:55 AM
A circle is the set of all those point in a plane whose distance from a fixed point remains constant. The fixed point is called the centre of the circle and the constant distance is known

New! Comments
Have your say about what you just read! Leave me a comment in the box below. Ask a Question or Answer a Question.