Trigonometric Ratios of Complementary Angles

Complementary angles and their trigonometric ratios:

We know from geometry if the sum of two angles is 90°, then one angle is called the complement of the other.

Two angles A and B are complementary if A + B = 90°. So, B = 90° - A.

For example, as 30° + 60° = 90°, 60° is called the complement of 30° and conversely, 30° is called the complement of 60°. 

Thus 27° is the complement of 60°; 43.5° is the complement of 46.5° etc.

Thus in general, (90° - θ) and θ are complementary angles. Trigonometric ratios of (90° - θ) are convertible to trigonometric ratios of θ.

Trigonometric Ratios of 90° - θ in Terms of Trigonometric ratios of θ

Let us see how we can find the trigonometrical ratios of 90° - θ, if we know those of θ°. 

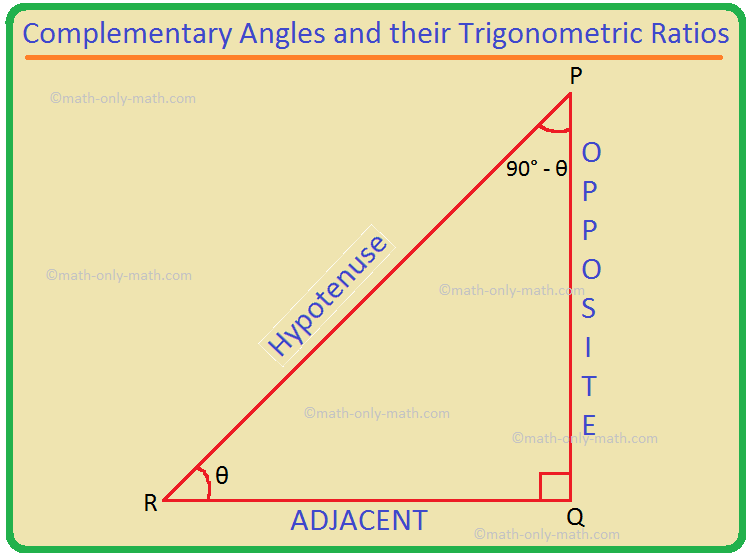
Let PQR be a right-angled triangle in which ∠Q is the right angle.

Let ∠PRQ = θ. Then, ∠QPR = 180° - (90° + θ) = 90° - θ.

1. sin (90° - θ) = cos θ

Here, sin (90° - θ) = \(\frac{QR}{PR}\) and cos θ = \(\frac{QR}{PR}\)

Therefore, sin (90° - θ) = cos θ.

2. cos (90° - θ) = sin θ

Here, cos (90° - θ) = \(\frac{PQ}{PR}\) and sin θ = \(\frac{PQ}{PR}\)

Therefore, cos (90° - θ) = sin θ.

3. tan (90° - θ) = cot θ

Here, tan (90° - θ) = \(\frac{QR}{PQ}\) and cot θ = \(\frac{QR}{PQ}\)

Therefore, tan (90° - θ) = cot θ.

4. csc (90° - θ) = sec θ

Here, csc (90° - θ) = \(\frac{PR}{QR}\) and sec θ = \(\frac{PR}{QR}\)

Therefore, csc (90° - θ) = sec θ

5. sec (90° - θ) = csc θ

Here, sec (90° - θ) = \(\frac{PR}{PQ}\) and csc θ = \(\frac{PR}{PQ}\)

Therefore, sec (90° - θ) = csc θ.

6. cot (90° - θ) = tan θ

Here, cot (90° - θ) = \(\frac{PQ}{QR}\) and tan θ = \(\frac{PQ}{QR}\)

Therefore, cot (90° - θ) = tan θ.

Thus, we have the following conversions of trigonometric ratios of (90° - θ) in terms of trigonometric ratios of θ.

For example, cos 37° can be expressed as sine of the complementary angle of 37° because

                                cos 37° = cos (90° - 53°) = sin 53°.

Note: The measure of an angle can be expressed in degrees (°) as well as in radians. The measure of an angle is π radians (where π is 3.14, approximately) if its measure in degrees is 180°. Thus, 180° = π radians. This is also written as 180° = π.

Therefore, 1° = \(\frac{π}{180}\)

              30° = \(\frac{π}{6}\)

              45° = \(\frac{π}{4}\)

              60° = \(\frac{π}{3}\)

              90° = \(\frac{π}{2}\), etc.

Therefore, we can write sin (90° - β) = sin (\(\frac{π}{2}\) – β) = cos β

                                   cos (90° - β) = cos (\(\frac{π}{2}\) – β) = sin β

                                   tan (90° - β) = tan (\(\frac{π}{2}\) – β) = cot β

                                   csc (90° - β) = csc (\(\frac{π}{2}\) – β) = sec β

                                   sec (90° - β) = sec (\(\frac{π}{2}\) – β) = csc β

                                   cot (90° - β) = cot (\(\frac{π}{2}\) – β) = tan β.

The values of trigonometrical ratios of 30° and 60°, which are complementary angles are compared below. This will help us to have a clear understanding of the relations shown before. 

sin 30° = cos 60° = \(\frac{1}{2}\)

cos 30° = sin 60° = \(\frac{\sqrt{3}}{2}\)

tan 30° = cot 60° = \(\frac{\sqrt{3}}{3}\)

csc 30° = sec 60° = 2

sec 30° = csc 60° = \(\frac{2\sqrt{3}}{3}\)

cot 30° = tan 60° = \(\sqrt{3}\)

Similarly, from the complementary angles formulae we get

sin 45° = cos 45° = \(\frac{\sqrt{2}}{2}\)

tan 45° = cot 45° = 1

csc 45 = sec 45° = \(\sqrt{2}\)

tan 45° = cot 45° = 1

Again, 

sin 90° = cos 0° = 1

cos 90° = sin 0° = 0

Problems on Trigonometric Ratios of Complementary Angles

Problems on evaluation using trigonometric ratios of complementary angles

1. Evaluate without using trigonometric table: \(\frac{sin 25°}{2 ∙ cos 65°}\)

Solution:

\(\frac{sin 25°}{2 ∙ cos 65°}\)

= \(\frac{sin 25°}{2 ∙ cos (90° - 25°)}\)

= \(\frac{sin 25°}{2 ∙ sin 25°}\); [since, cos (90° - θ) = sin θ]

= \(\frac{1}{2}\).

2. Evaluate without using trigonometric table: tan 38° ∙ tan 52°

Solution:

tan 38° ∙ tan 52°

= tan 38° ∙ tan (90° - 38°)

= tan 38° ∙ cot 38°; [Since, tan (90° - θ) = cot θ]

= tan 38° ∙ \(\frac{1}{tan 38°}\)

= 1.

3. Evaluate without using trigonometric table: \(\frac{sin 67°}{cos 23°}\) - \(\frac{sec 12°}{csc 78°}\)

Solution:

\(\frac{sin 67°}{cos 23°}\) - \(\frac{sec 12°}{csc 78°}\)

= \(\frac{sin 67°}{cos (90° - 67°)}\) - \(\frac{sec 12°}{csc (90° - 12°)}\)

= \(\frac{sin 67°}{cos (90° - 67°)}\) - \(\frac{sec 12°}{csc (90° - 12°)}\)

= \(\frac{sin 67°}{sin 67°}\) - \(\frac{sec 12°}{sec 12°}\)

[Since, cos (90° - θ) = sin θ and csc (90° - θ) = sec θ]

= 1 - 1

= 0.

4. If cos 39° = \(\frac{x}{\sqrt{x^{2} + y^{2}}}\), what is the value of tan 51°?

Solution:

Given that cos 39° = \(\frac{x}{\sqrt{x^{2} + y^{2}}}\)

Therefore, sin² 39° = 1 -  \(\frac{x^{2}}{x^{2} + y^{2}}\)

                            = \(\frac{x^{2} + y^{2} - x^{2}}{x^{2} + y^{2}}\)

                            = \(\frac{y^{2}}{x^{2} + y^{2}}\)

Therefore, sin 39° = \(\frac{y}{\sqrt{x^{2} + y^{2}}}\), (negative value is not acceptable)

Now, tan 51° = tan (90° - 39°)

                    =  cot 39°

                    = \(\frac{cos 39°}{sin 39°}\)

                    = cos 39° ÷ sin 39°

                    = \(\frac{x}{\sqrt{x^{2} + y^{2}}}\) ÷ \(\frac{y}{\sqrt{x^{2} + y^{2}}}\)

                    = \(\frac{x}{y}\).

5. If cos 37° = x then find the value of tan 53°.

Solution:

tan 53°

= tan (90° - 37°)

= cot 37°; [Since, tan (90° - θ) = cot θ]

= \(\frac{cos 37°}{sin 37°}\)

= \(\frac{x}{sin 37°}\) ................ (i)

Now, sin² 37° = 1 - cos² 37°; [since, 1 - cos² θ = sin² θ]

Therefore, sin 37° = \(\sqrt{1 - cos^{2} 37°}\)

                           = \(\sqrt{1 - x^{2}}\)

Therefore, from (i), tan 53° = \(\frac{x}{\sqrt{1 - x^{2}}}\).

6. If sec  ϕ = csc  β and 0° < (ϕ, β) < 90°, find the value of sin (ϕ + β).

Solution:

sec  ϕ = csc  β

⟹ \(\frac{1}{cos ϕ}\) = \(\frac{1}{sin β}\)

⟹ cos ϕ = sin β

⟹ cos ϕ = cos (90° - β)

⟹ ϕ = 90° - β

⟹ ϕ + β = 90°

Therefore, sin (ϕ + β) = sin 90° = 1.

7. Find the value of sin² 15° + sin² 25° + sin² 33° + sin² 57° + sin² 65° + sin² 75°.

Solution:

sin² (90° - 75°) + sin² (90° - 65°) + sin² (90° - 57°) + sin² 57° + sin² 65° + sin² 75°.

= cos² 75° + cos² 65° + cos² 57° + sin² 57° + sin² 65° + sin² 75°.

= (sin² 57° + cos² 75°) + (sin² 65° + cos² 65°) + (sin² 57° + cos² 57°)

= 1 + 1 + 1; [Since, sin² θ + cos² θ = 1]

= 3.

8. If tan 49° ∙ cot (90° - θ) = 1, find θ.

Solution:

tan 49° ∙ cot (90° - θ) = 1

⟹ tan 49° ∙ tan θ = 1; [Since, cot (90° - θ) = tan θ]

⟹ tan θ = \(\frac{1}{tan 49°}\)

⟹ tan θ = cot 49°

⟹ tan θ = cot (90° - 41°)

⟹ tan θ = tan 41°

⟹ θ = 41°

Therefore, θ = tan 41°.

Problems on establishing equality using trigonometric ratios of complementary angles

9. Prove that sin 33° cos 77° = cos 57° sin 13°

Solution:

LHS = sin 33° cos 77°

       = sin (90° - 57°) cos (90° - 13°)

       = cos 57° sin 13°

       = RHS. (Proved).

10. Prove that tan 11° + cot 63° = tan 27° + cot 79°

Solution:

LHS = tan 11° + cot 63°

       = tan (90° - 79°) + cot (90° - 27°)

       = cot 79° + tan 27°

       = tan 27° + cot 79°

       = RHS. (Proved).

Problems on establishing identities and simplification using trigonometric ratios of complementary angles

11. If P and Q are two complementary angles, show that

(sin P + sin Q)² = 1 + 2 sin P cos P

Solution:

Since P are Q are complementary angles,

Therefore, sin Q = sin (90° - P) = cos P

Therefore, (sin P + sin Q)² = (sin P + cos P)² 

                                       = sin² P + cos² P + 2 sin P cos P

                                       = (sin² P + cos² P) + 2 sin P cos P

                                       = 1 + 2 sin P cos P

12. Simplify: \(\frac{sin (\frac{π}{2} - θ) ∙ cot (\frac{π}{2} - θ)}{sin θ}\)

Solution: 

\(\frac{sin (\frac{π}{2} - θ) ∙ cot (\frac{π}{2} - θ)}{sin θ}\)

= \(\frac{cos θ ∙ tan θ}{sin θ}\), [Since sin (\(\frac{π}{2}\) - θ) = sin (90° - θ) = cos θ and cot (\(\frac{π}{2}\) - θ) = cot (90° - θ) = tan θ]

= \(\frac{cos θ ∙ \frac{sin θ}{cos θ}}{sin θ}\)

=  \(\frac{sin θ}{sin θ}\)

= 1.

13. Prove that, sin² 7° + sin² 83°

Solution:

sin 83° = sin (90° - 7°) 

           = cos 7°; [since, sin (90° - θ) = cos θ]

LHS = sin² 7° + sin² 83°

      = sin² 7° + cos² 7°, [Since, sin 83° = cos 7°]

      = 1 = RHS (Proved).

14. In a ∆PQR, prove that sin \(\frac{P + Q}{2}\) = cos \(\frac{R}{2}\).

Solution:

We know that sum of the three angles of a triangle is 180°.

i,e., P + Q + R = 180°

⟹  P + Q = 180° - R

Now, 

LHS = sin \(\frac{P + Q}{2}\) 

      = sin \(\frac{180° - R}{2}\) 

      = sin (90° - \(\frac{R}{2}\))

      = cos \(\frac{R}{2}\) = RHS (Proved). 

15. Prove that tan 15° + tan 75° = \(\frac{sec^{2} 15°}{\sqrt{sec^{2} 15° - 1}}\).

Solution:

LHS = tan 15° + tan (90° - 15°)

       = tan 15° + cot 15°

       = tan 15° + \(\frac{1}{tan 15°}\)

       = \(\frac{tan^{2} 15° + 1}{tan 15°}\)

       = \(\frac{sec^{2} 15°}{\sqrt{sec^{2} 15° - 1}}\) = RHS (Proved).

Learn more about Trigonometrical Ratios of Complementary Angles.

10th Grade Math

From Trigonometric Ratios of Complementary Angles to HOME PAGE