Subscribe to our ▶️ YouTube channel 🔴 for the latest videos, updates, and tips.
Comparing and Ordering Fractions (Like and Unlike Fractions)
In comparing and ordering fractions, we will learn how to compare and order fractions step-by-step. We cover easy tricks such as comparing fractions with the same denominator, the same numerator, using cross multiplication, and converting fractions to like denominators. This lesson will help you quickly decide which fraction is bigger or smaller and how to arrange fractions in ascending and descending order.
Comparing and Ordering Fractions is perfect for Class 4, 5, and 6 students, competitive exam preparation, and anyone who wants to master fractions in a simple way.
Comparing fractions means finding which fraction is greater (>), smaller (<), or equal (=).
Ordering fractions means arranging them in ascending (smallest to greatest) or descending (greatest to smallest) order.
1. Comparing Like Fractions:
To compare like fractions, i.e., fractions having the same denominators, compare the numerators. The fraction having greater numerator is greater than the fraction having smaller numerator.
For example:
(i) \(\frac{8}{15}\) > \(\frac{7}{15}\)
(ii) \(\frac{2}{7}\) < \(\frac{6}{7}\)
(iii) \(\frac{21}{35}\) > \(\frac{11}{35}\)
2. Comparing Unlike Fractions
Unlike fractions are compared in two ways:
(a) When the unlike fractions have the same numerator, the fraction having greater denominator is smaller than the fraction having the smaller denominator.
For example:
(i) \(\frac{7}{11}\) > \(\frac{7}{12}\)
(ii) \(\frac{27}{31}\) > \(\frac{27}{35}\)
(ⅲ) \(\frac{13}{20}\) > \(\frac{13}{25}\)
(b) When the unlike fractions have different numerators, first express them to a common denominator by taking LCM of their denominators. Then compare their numerators.
For example:
Let us compare \(\frac{5}{12}\) and \(\frac{7}{16}\).
Now find the LCM of 12 and 16.
LCM of 12 and 16 is 48.
Therefore, \(\frac{5}{12}\) = \(\frac{5 × 4}{12 × 4}\) = \(\frac{20}{48}\)
and \(\frac{7}{16}\) = \(\frac{7 × 3}{16 × 3}\) = \(\frac{21}{48}\)
Since 21 > 20, therefore, \(\frac{21}{48}\) > \(\frac{20}{48}\)
or, \(\frac{7}{16}\) > \(\frac{5}{12}\)
or, \(\frac{5}{12}\) < \(\frac{7}{16}\).
Such fractions can also be compared by cross multiplication.
Let \(\frac{a}{b}\) and \(\frac{c}{d}\) be two fractions:
(i) If ad > bc, \(\frac{a}{b}\) > \(\frac{c}{d}\)
(ii) If ad < bc , \(\frac{a}{b}\) < \(\frac{c}{d}\)
(iii) If ad = bc, \(\frac{a}{b}\) = \(\frac{c}{d}\)
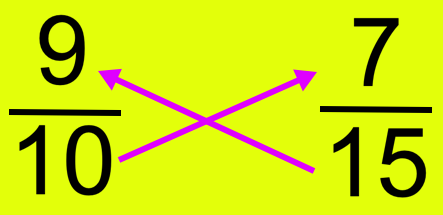
For example, compare the fractions \(\frac{9}{10}\) and \(\frac{7}{15}\)
The cross products are: 9 × 15 = 135 and 10 × 7 = 70
Since 135 > 70 therefore, \(\frac{9}{10}\) > \(\frac{7}{15}\).
Solved Examples on Comparison of Fractions:
1. State which is smaller \(\frac{4}{9}\) or \(\frac{7}{11}\).
Solution:
First find the LCM of the denominators 9 and 11.
The LCM of denominators 9 and 11 is 99.
Therefore, \(\frac{4}{9}\) = \(\frac{4 × 11}{9 × 11}\) = \(\frac{44}{99}\)
and \(\frac{7}{11}\) = \(\frac{7 × 9}{11 × 9}\) = \(\frac{63}{99}\)
Since 44 < 63, therefore, \(\frac{44}{99}\) < \(\frac{63}{99}\)
or, \(\frac{4}{9}\) < \(\frac{7}{11}\).
Hence, \(\frac{4}{9}\) is smaller.
2. State which is greater \(\frac{2}{8}\) or \(\frac{3}{7}\).
Solution:
First find the LCM of the denominators 8 and 7.
The LCM of denominators 8 and 7 is 56.
Therefore, \(\frac{2}{8}\) = \(\frac{2 × 7}{8 × 7}\) = \(\frac{14}{56}\)
and \(\frac{3}{7}\) = \(\frac{3 × 8}{7 × 8}\) = \(\frac{24}{56}\)
Since 24 > 14, therefore, \(\frac{24}{56}\) > \(\frac{14}{56}\)
or, \(\frac{3}{7}\) > \(\frac{2}{8}\).
Hence, \(\frac{3}{7}\) is greater.
3. Arrange the following fractions in ascending order:
(i) \(\frac{21}{19}\), \(\frac{4}{19}\), \(\frac{11}{19}\), \(\frac{6}{19}\), \(\frac{25}{19}\), \(\frac{16}{19}\)
(ii) \(\frac{24}{25}\), \(\frac{23}{25}\), \(\frac{22}{25}\), \(\frac{21}{25}\), \(\frac{30}{25}\)
Solution:
(i) Writing the numerators in ascending order, we get:
4 < 6 < 11 < 16 < 21 < 25
Now write the above numerators with their denominators as:
\(\frac{4}{19}\) < \(\frac{6}{19}\) < \(\frac{11}{19}\) < \(\frac{16}{19}\) < \(\frac{21}{19}\) < \(\frac{25}{19}\), which are in ascending order.
(ii) Writing the numerators in ascending order, we get:
21 < 22 < 23 < 24 < 30
Now write the above numerators with their denominators as:
\(\frac{21}{25}\) < \(\frac{22}{25}\) < \(\frac{23}{25}\) < \(\frac{24}{25}\) < \(\frac{30}{25}\), which are in ascending order.
4. Write the following fractions in descending order:
(i) \(\frac{37}{45}\), \(\frac{41}{45}\), \(\frac{5}{45}\), \(\frac{21}{45}\), \(\frac{60}{45}\)
(ii) \(\frac{9}{11}\), \(\frac{1}{11}\), \(\frac{2}{11}\), \(\frac{5}{11}\), \(\frac{4}{11}\)
Solution:
(i) Writing the numerators in descending order, we get:
60 > 41 > 37 > 21 > 5
Now write the above numerators with their denominators as:
\(\frac{60}{45}\) > \(\frac{41}{45}\) > \(\frac{37}{45}\) > \(\frac{21}{45}\) > \(\frac{5}{45}\), which are in descending order.
(ii) Writing the numerators in descending order, we get:
9 > 5 > 4 > 2 > 1
Now write the above numerators with their denominators as:
\(\frac{9}{11}\) > \(\frac{5}{11}\) > \(\frac{4}{11}\) > \(\frac{2}{11}\) > \(\frac{1}{11}\), which are in descending order.
5. Nairitee takes 2\(\frac{1}{5}\) minutes in walking under the flyover. Nitheeya takes \(\frac{7}{4}\) minutes to do same. Who takes more time?
Solution:
Time taken by Nairitee = 2\(\frac{1}{5}\) minutes = \(\frac{11}{5}\) minutes
Time taken by Nitheeya = \(\frac{7}{4}\) minutes
Now find the LCM of 5 and 4.
Therefore, the LCM of 5 and 4 is 20.
Now, \(\frac{11}{5}\) = \(\frac{11 × 4}{5 × 4}\) = \(\frac{44}{20}\)
and \(\frac{7}{4}\) = \(\frac{7 × 5}{4 × 5}\) = \(\frac{35}{20}\)
Since 44 > 35, therefore, \(\frac{44}{20}\) > \(\frac{35}{20}\)
or, \(\frac{11}{5}\) > \(\frac{7}{4}\).
Hence, Nairitee takes more time.
6. Priyanka read 137 pages of a book containing 250 pages. Tuhin read \(\frac{3}{5}\) of the same book. Who read less number of pages?
Solution:
Number of pages that Priyanka read = 137.
Number of pages that Tuhin read = \(\frac{3}{5}\) of the total number of pagess in the book.
= \(\frac{3}{5}\) × 250
= \(\frac{3}{5}\) × \(\frac{250}{1}\)
= \(\frac{750}{5}\)
= 150
Hence, Priyanka read less number of pages.
From Comparing and Ordering Fractions (Like and Unlike Fractions) to HOME PAGE
Didn't find what you were looking for? Or want to know more information about Math Only Math. Use this Google Search to find what you need.
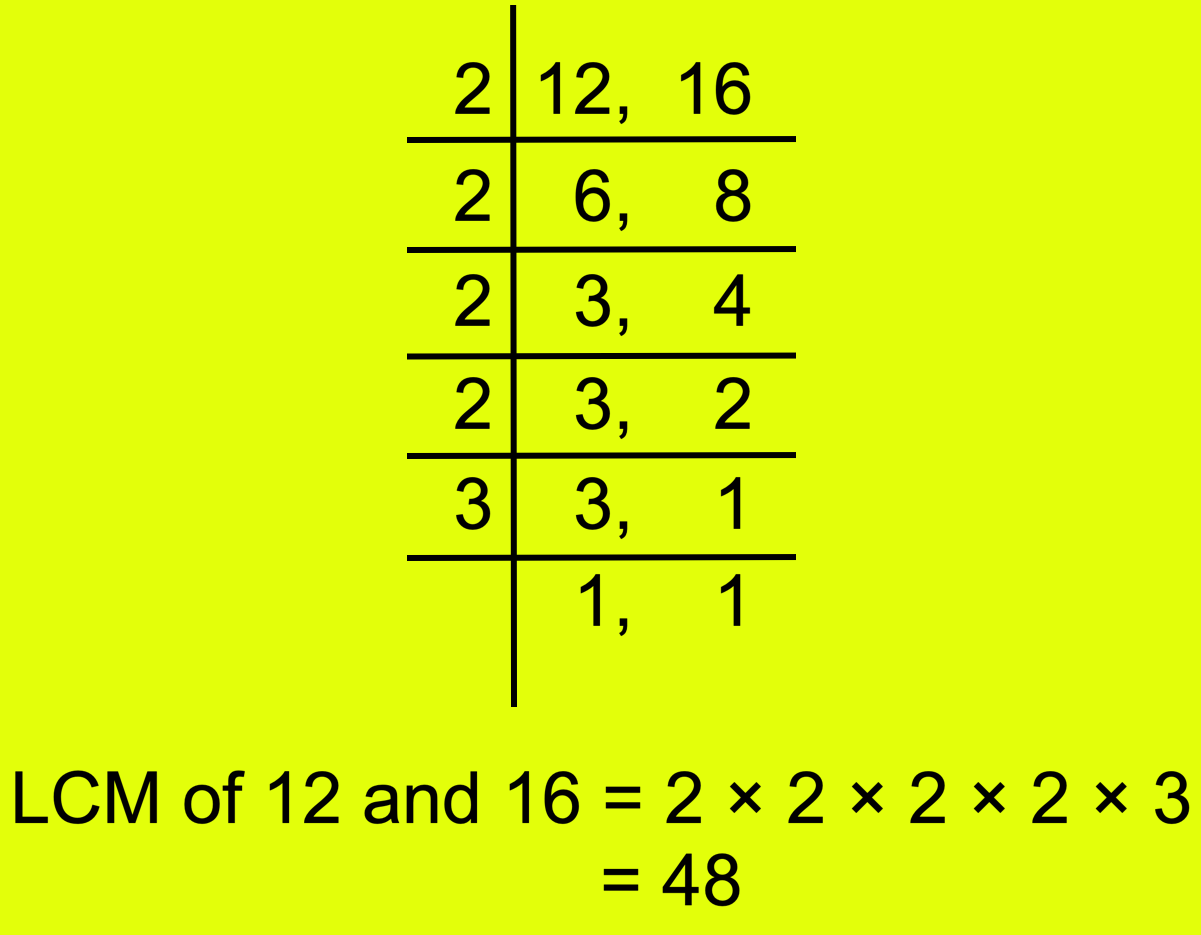
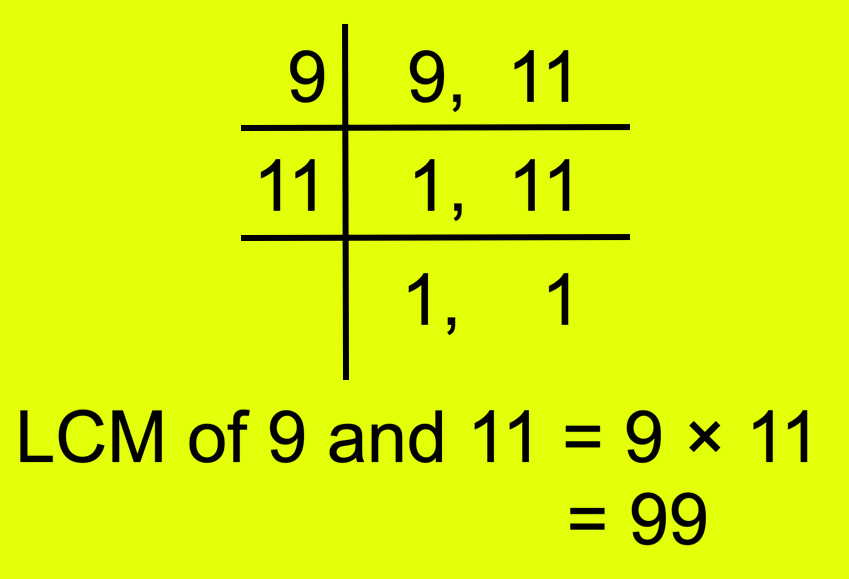
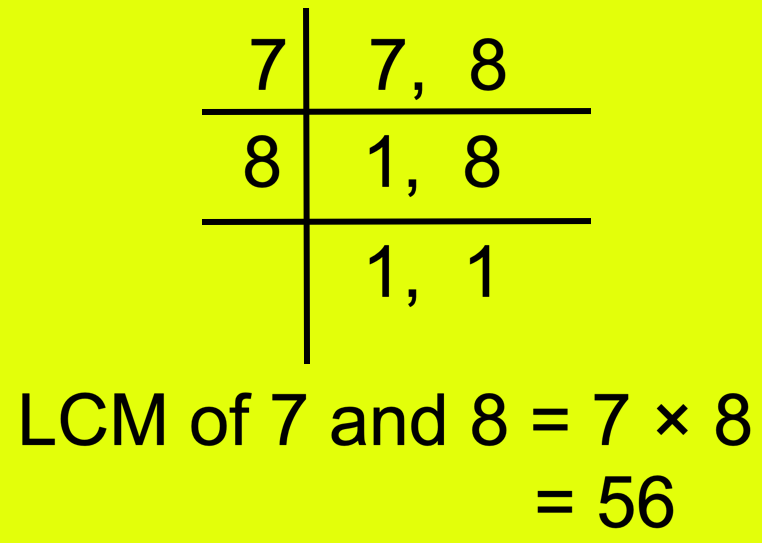
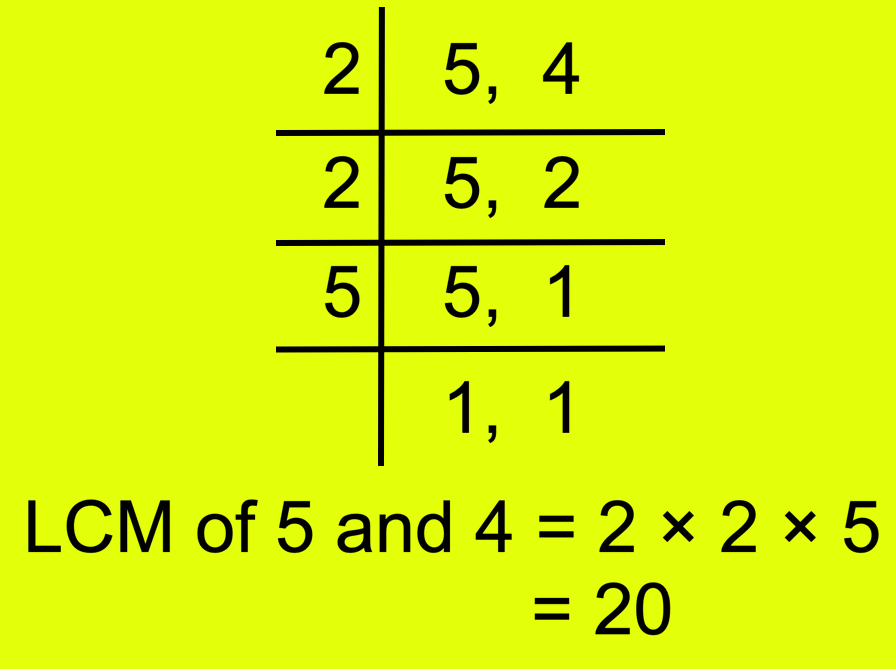


New! Comments
Have your say about what you just read! Leave me a comment in the box below. Ask a Question or Answer a Question.