Subscribe to our ▶️YouTube channel🔴 for the latest videos, updates, and tips.
Home | About Us | Contact Us | Privacy | Math Blog
Surds
We will discuss here about surds and its definition.
First let us recall about rational number and irrational number.
Before defining surds, we will first define what are rational and irrational number?
Rational number: A number of the form p/q, where p (may be a positive or negative integer or zero) and q (taken as a positive integer) are integers prime to each other and q not equal to zero is called a rational number or commensurable quantity.
Rational numbers are the numbers which can be expressed in the form of p/q where p is a positive or negative integer or zero and q is a positive or negative integer but not equal to zero.
Like: 57, 3, - 23 are the examples of rational numbers.
For example, each of the numbers 7, 35, 0.73, √25 etc. is a rational number. Evidently, the number 0 (zero) is a rational number.
Irrational number: A number which cannot be expressed in the form p/q where p and q are integers and q ≠ 0, is called an irrational number or incommensurable quantity.
Irrational numbers are the numbers which can’t be expressed in the form of p/q where p and q are integers and q ≠ 0. Irrational numbers have infinite numbers of decimals of non-recurring nature.
Like: π, √2, √5 are the irrational numbers.
For example, each of the numbers √7, ∛3, 5√13 etc. is an irrational number.
Definitions
of surd: A root of a positive real quantity is called a surd if its value
cannot be exactly determined.
Surds are the irrational numbers which are roots of positive integers and the value of roots can’t be determined. Surds have infinite non-recurring decimals. Examples are √2, √5, ∛17 which are square roots or cube roots or nth root of any positive integer.
For example, each of the quantities √3, ∛7, ∜19, (16)^25 etc. is a surd.
From the definition it is evident that a surd is an incommensurable quantity, although its value can be determined to any degree of accuracy. It should be noted that quantities √9, ∛64, ∜(256/625) etc. expressed in the form of surds are commensurable quantities and are not surds (since √9 = 3, ∛64 = 4, ∜(256/625) = 45 etc.). In fact, any root of an algebraic expression is regarded as a surd.
Thus, each of √m, ∛n, 5√x2 etc. may be regarded as a surd when the value of m ( or n or x) is not given. Note that √m = 8 when m = 64; hence, in this case √m does not represent a surd. Thus, √m does not represent surd for all values of m.
∛8 or ∜81 can be simplified into 2 or 3 which are rational numbers or positive integers, ∛8 or ∜81 are not surds. But the value of √2 is 1.41421356…., so the decimals continue up to infinite numbers and non-recurring in nature, so √2 is a surd. π and e have also values which contain decimals up to infinite numbers but they are not root of positive integers so they are irrational numbers but not surds. So all surds are irrational numbers but all irrational numbers are not surds.
If x is a positive integer with nth root, then n√x is a surd of nth order when the value of n√x is irrational. In n√x expression n is the order of surd and x is called as radicand.
The reason that we leave surds in root form as the values can’t be simplified, so during problem solving with surds, we normally try to convert the surds to more simplified forms and whenever necessary we can take approximate value of any surd up to any decimal to calculate.
Note: All surds are irrationals but all irrational numbers are not surds. Irrational numbers like π and e, which are not the roots of algebraic expressions, are not surds.
Now we solve some problems on surds to understand more on surds.
1. Express √2 as a surd of order 4.
Solution
√2 = 212
=21×22×2
= 224
= 414
= 4√4
4√4 is a surd of order 4.
2. Find which are surds from the following numbers?
√24, ∛64 x √121, √50
Solution:
√24 = √4×6
= 2√2 × √3
So √24 is a surd.
∛64 × √121 = 3√43 × √112
= 4 × 11
= 44
So ∛64 x √121 is rational and not a surd.
√50 = √2×25
= √2×52
= 5√2
So √50 is a surd.
If the denominator of a expression is a surd, then often it requires to convert the denominator to rational number. This process is called rationalizing or rationalization of surd. This can be done by multiplying a suitable factor to the denominator to convert the expression in to a more simplified form. This factor is called as rationalizing factor. If the product of two surds is a rational number, then each surd is a rationalizing factor to the other surd.
For example 12+√3 is expression, where the denominator is a surd.
12+√3
= 1×(2−√3)(2+√3)×(2−√3)
= (2−√3)4−3
= 2 - √3
So the rationalizing factor of (2 + √3) is (2 - √3).
11 and 12 Grade Math
From Surds to HOME PAGE
Didn't find what you were looking for? Or want to know more information about Math Only Math. Use this Google Search to find what you need.
Recent Articles
-
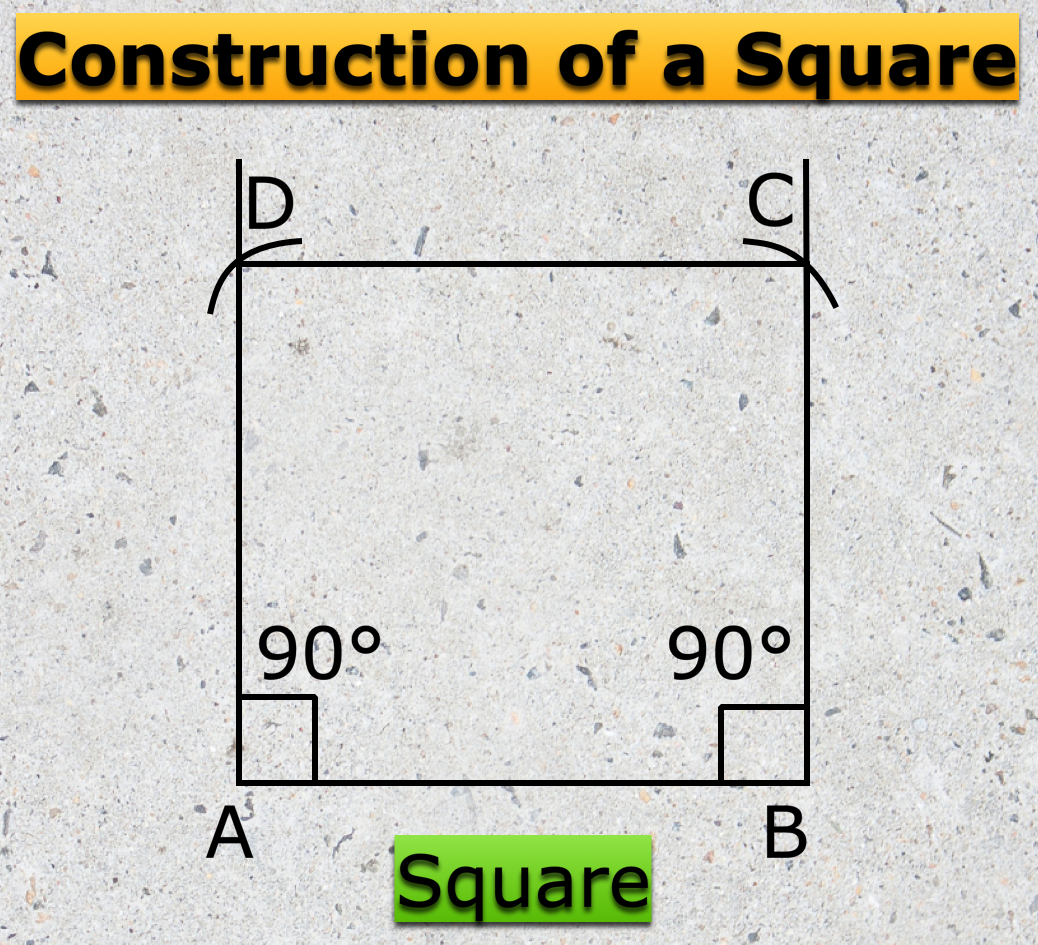
Formation of Square and Rectangle | Construction of Square & Rectangle
Jul 15, 25 02:46 AM
In formation of square and rectangle we will learn how to construct square and rectangle. Construction of a Square: We follow the method given below. Step I: We draw a line segment AB of the required… -
5th Grade Quadrilaterals | Square | Rectangle | Parallelogram |Rhombus
Jul 15, 25 02:01 AM
Quadrilaterals are known as four sided polygon.What is a quadrilateral? A closed figure made of our line segments is called a quadrilateral. For example: -
Formation of Numbers | Smallest and Greatest Number| Number Formation
Jul 14, 25 01:53 AM
In formation of numbers we will learn the numbers having different numbers of digits. We know that: (i) Greatest number of one digit = 9, -
5th Grade Geometry Practice Test | Angle | Triangle | Circle |Free Ans
Jul 14, 25 01:53 AM
In 5th grade geometry practice test you will get different types of practice questions on lines, types of angle, triangles, properties of triangles, classification of triangles, construction of triang… -
5th Grade Circle Worksheet | Free Worksheet with Answer |Practice Math
Jul 11, 25 02:14 PM
In 5th Grade Circle Worksheet you will get different types of questions on parts of a circle, relation between radius and diameter, interior of a circle, exterior of a circle and construction of circl…

New! Comments
Have your say about what you just read! Leave me a comment in the box below. Ask a Question or Answer a Question.