Construction of Quadrilaterals

In construction of quadrilaterals we will learn how to construct a quadrilateral. We know that a quadrilateral has ten parts in all: four sides, four angles and two diagonals. To construct a quadrilateral, we shall need data about five specified parts of it.

We consider the following five cases and explain the construction in each case by an example. 

We divide the required quadrilateral into two triangles which can be easily constructed. 

These two triangles together will form a quadrilateral. 

I. Construction of quadrilaterals when four sides and one diagonal are given: 

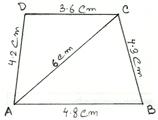
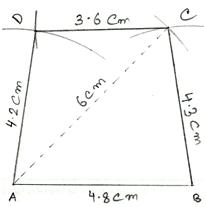
1. Construct a quadrilateral ABCD in which AB = 4.8 cm, BC = 4.3 cm, CD = 3.6 cm, AD = 4.2 cm and diagonal AC = 6 cm. 

Solution:

Solution:

First we draw a rough sketch of quadrilateral ABCD and write down its dimensions, as shown.

We may divide it into two triangles, namely ∆ABC and ∆ACD. (Rough Sketch) →

Steps of Construction:

Step 1: Draw AB = 4.8 cm.

Step 2: With A as center and radius equal to 6 cm, draw an arc.

Step 3: With B as center and radius equal to 4.3 cm, draw another arc, cutting the previous arc at C.

Step4: Join BC.

Step 5: With A as center and radius equal to 4.2 cm, draw an arc.

Step 6: With C as center and radius equal to 3.6 cm, draw another arc, cutting the previous arc at D.

Step 7: Join AD and CD.

Then, ABCD is the required quadrilateral.

II. Construction of quadrilaterals when three sides and two diagonals are given:

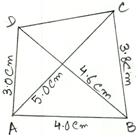
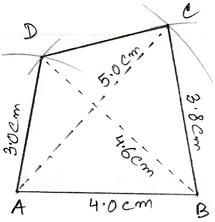
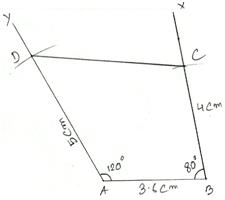
2. Construct a quadrilateral ABCD in which AB = 4 cm BC = 3.8 cm, AD = 3 cm, diagonal AC = 5 cm and diagonal BD = 4.6 cm.

Solution:

First we draw a rough sketch of quadrilateral ABCD and write down its dimensions, as shown.

We may divide it into two triangles, namely ∆ABC and ∆ABD. (Rough Sketch) →

Steps of Construction:

Step 1: Draw AB = 4 cm.

Step 2: With A as center and radius equal to 5 cm, draw an arc.

Step 3: With B as center and radius equal to 3.8 cm, draw another arc, cutting the previous arc at C.

Step 4: Join BC.

Step 5: With A as center and radius equal to 3 cm, draw an arc.

Step 6: With B as center and radius equal to 4.6 cm draw another arc, cutting the previous arc at D.

Step 7: Join AD and CD.

Then, ABCD is the required quadrilateral.

III. Construction of quadrilaterals when three sides and two included angles are given: 

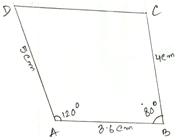
3. Construct a quadrilateral ABCD in which AB = 3.6 cm, ∠ABC = 80°, BC = 4 cm, ∠BAD = 120° and AD = 5 cm. 

Solution:

First we draw a rough sketch of quadrilateral ABCD and write down its dimensions, as shown (Rough Sketch) →

Steps of Construction:

Step 1: Draw AB = 3.6 cm.

Step 2: Make ∠ABX = 80°.

Step 3: With B as center and radius equal to 4 cm, draw an arc, cutting BX at C.

Step 4: Make ∠BAY = 120°.

Step 5: With A as center and 5 cm as radius, draw an arc, cutting AY at D. Step 6: Join CD.

Then, ABCD is the required quadrilateral.

IV. Construction of quadrilaterals when two adjacent sides and three angles are given:

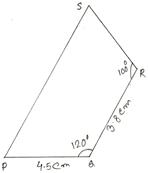
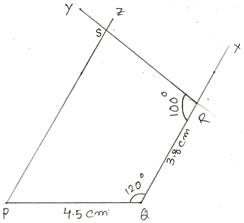
4. Construct a quadrilateral PQRS in which PQ = 4.5 cm ∠PQR = 120°, QR = 3.8 cm, ∠QRS = 100° and ∠QPS = 60°.

Solution:

First we draw a rough sketch of quadrilateral PQRS and write down its dimensions, as shown.
(Rough Sketch) →

Steps of Construction:

Step 1: Draw PQ = 4.5 cm.

Step 2: Make ∠PQX = 120°.

Step 3: With Q as center and radius 3.8 cm, draw an arc, cutting QX at R. Join QR.

Step 4: Make ∠QRY = 100°.

Step 5: ∠QPZ = 60° so that PZ and RY intersect each other at the point S.

Then, PQRS is the required quadrilateral.

V. Construction of quadrilaterals when four sides and one angle are given:

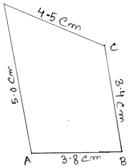
5. Construct a quadrilateral ABCD in which AB = 3.8 cm, BC = 3.4cm, CD = 4.5 cm, AD = 5cm and ∠B = 80°.

Solution:

First we draw a rough sketch of quadrilateral ABCD and write down its dimensions, as shown.
(Rough Sketch) →

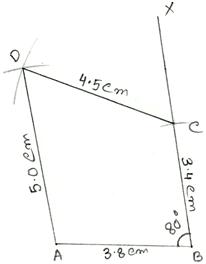
Steps of Construction:

Step 1: Draw AB = 3.8 cm.

Step 2: Make ∠ABX = 80°.

Step 3: From B, set off BC = 3.4 cm.

Step 4: With A as center and radius equal to 5 cm draw an arc.

Step 5: With C as center and radius equal to 4.5 cm, draw another arc, cutting the previous arc at D.

Step 5: Join AD and CD.

Then ABCD is the required quadrilateral.

● Related Concepts on Quadrilateral

● What is Quadrilateral?

● Different Types of Quadrilaterals

● Construction of Quadrilaterals

● Construct Different Types of Quadrilaterals

● Quadrilateral - Worksheets

● Quadrilateral Worksheet

● Worksheet on Construction on Quadrilateral

● Worksheet on Different Types of Quadrilaterals

8th Grade Math Practice

From Construction of Quadrilaterals to HOME PAGE