Subscribe to our YouTube channel for the latest videos, updates, and tips.
Home | About Us | Contact Us | Privacy | Math Blog
Comparison of Three-digit Numbers
Comparing 3-Digit Numbers:
We have already learnt how to compare 2-digit numbers. We also know the symbols to show the greater number and the smaller number.
How to compare 3-digit numbers?
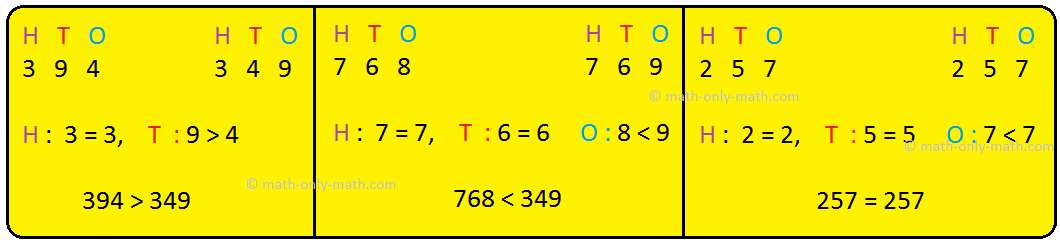
• First compare the digits in the hundreds place.
So, 835 > 792.
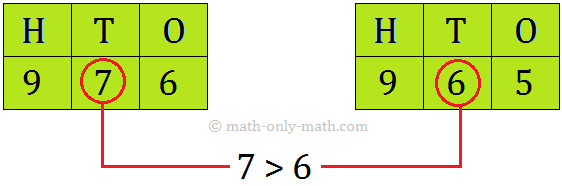
• If the digits in the hundreds place are the same, compare the digits in the tens place.
So, 976 > 965.
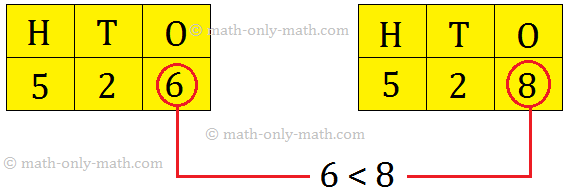
• If the digits in the hundreds and tens places are the same, compare the digits in the ones place.
So, 526 < 528.
Remember:
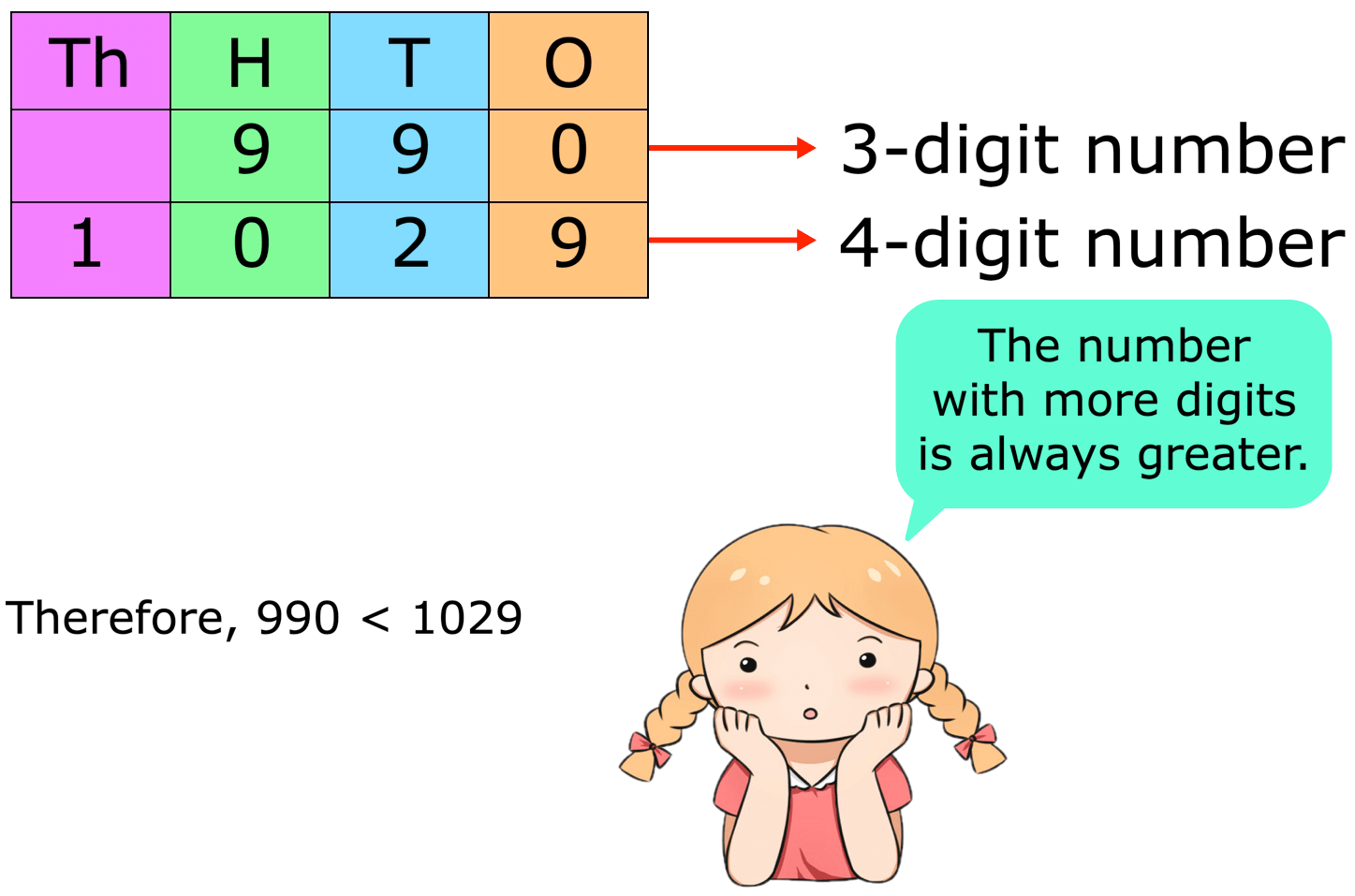
The number which has more digits is greater number.
For Example: 187 < 25
9 < 15
Comparing 3-Digit Numbers Video
Subscribe to our YouTube channel for the latest videos, updates, and tips.
1. Compare the numbers 396 and 403.
Method I: Using the number line
We can see that the number 403 comes later on the number line than the number 396. So, 403 > 396.
Method II: Using Place Value
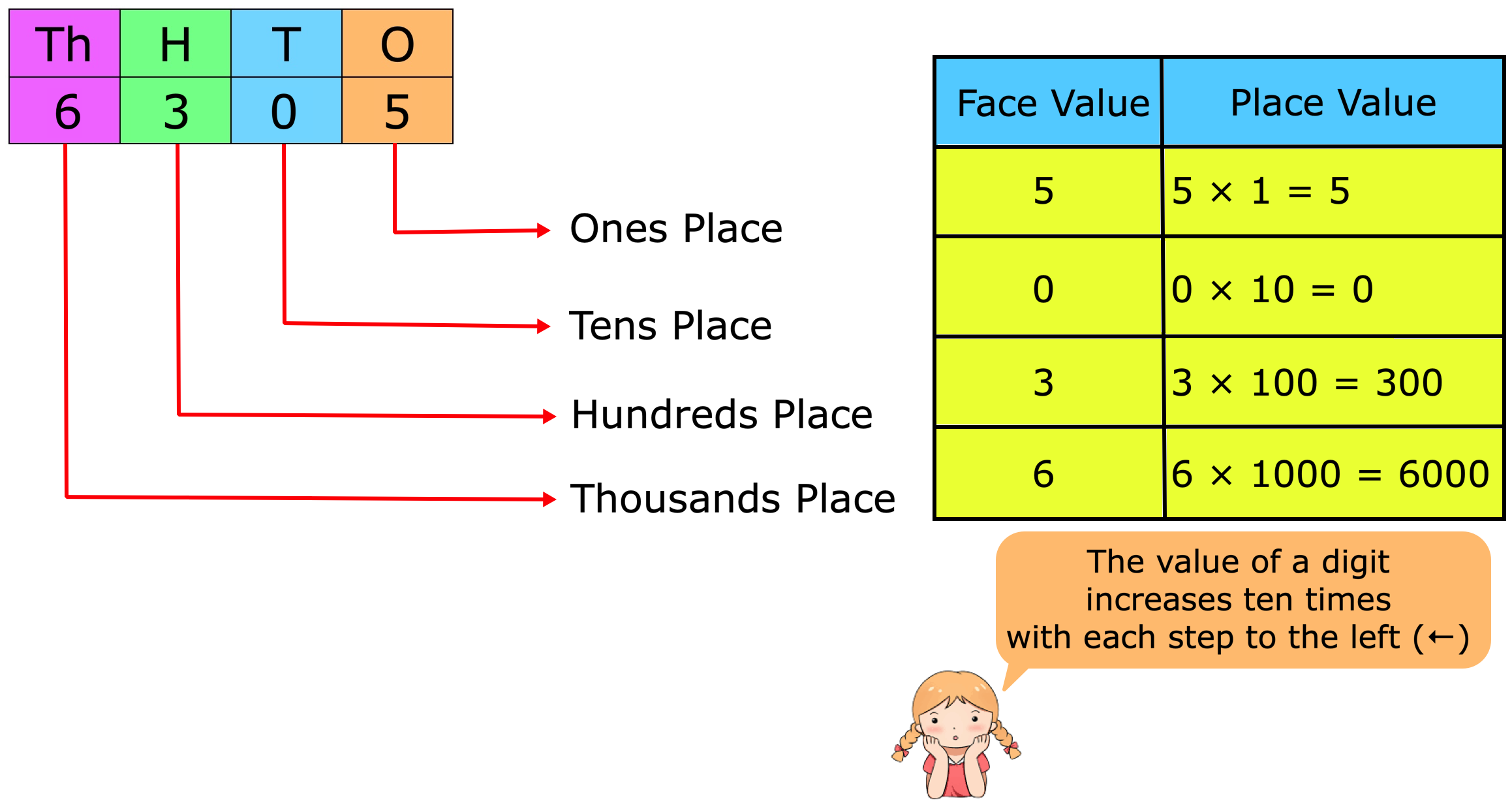
The number with the greater digit in the bigger place is bigger.
The hundreds place has 4 in the number 403 while the hundreds place has 3 in the number 396.
As 4 > 3, 403 > 396.
2. Compare the numbers 287 and 78.
We know the number with more number of digits is always greater and the number with less number of digits is always smaller.
Since 287 is a 3-digit number and 78 is a 2-digit number, 287 > 78
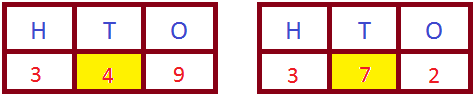
3. Compare the numbers 349 and 372.
Here, both the digits in the hundreds place are the same. So, we compare the digits in the tens place.
The tens place has 4 in the number 349. The tens place has 7 in the number 372.
As 4 < 7, 349 < 372.
4. Compare the numbers 486 and 483.
Here, the digits in the hundreds place and the tens place of the two numbers are the same. So, we compare the digits in the ones place.
As 6> 3, 486 > 483.
Note: First, compare the hundreds. Then, compare the tens. Finally, compare the ones.
What are the rules for the comparison of three-digit numbers?
(i) The numbers having less than three digits are always smaller than the numbers having three digits as:
100 > 99 , 100 > 9 or 9 < 100 , 99 < 100
125 > 75 , 327 > 59 , 107 > 8 , etc.
(ii) If both the numbers have the same numbers (three) of digits, then the digits on the extreme left are compared.
(a) If the third digit from the right (Hundred-place digit) of a number is greater than the third digit from the right (Hundred-place digit) of the other number then the number having the greater third digit from the right, is the greater one.
Thus, the number having the greater digit to its extreme left, is the greater one,
as:
913 > 899 , 749 > 698 , 576 > 425
(b) If the numbers have the same third digits from the
right, then the digits at ten’s place are compared and rules to compare
two-digit numbers are considered.
958 > 949 , 876 > 867 , 564 > 559
If digits at Hundred-place and ten’s place are equal, the rules to compare single digit numbers are considered.
958 > 956 , 876 > 875 , 634 > 630
Arranging 3-Digit Numbers:
How to arrange 3-digit numbers in ascending and descending order:
(i) Arranging the numbers 237, 185, 271, 146, 329 in ascending order:
The numbers are arranged in ascending order 146, 185, 237, 271, 329.
(ii) Arranging the numbers 204, 318, 432, 155, 296 in descending order:
The numbers are arranged in descending order 432, 318, 296, 204, 155.
(iii) Arranging the numbers 471, 295, 311, 163, 239 in ascending order:
The numbers are arranged in ascending order 163, 239, 295, 311, 471.
(iv) Arranging the numbers 374, 198, 282, 351, 461 in descending order:
The numbers are arranged in descending order 461, 374, 351, 282, 198.
Thus, any four-digit number is always greater than a three-digit number.
1000 > 999 , 2000 > 700 , 3150 > 550 , etc.
● Numbers are compared from left to right.
● If the digits are equal at a place then compare the right digit at the next place.
For example:
1. Arrange the numbers 932, 122, 952, 942 in ascending order.
First find the smallest number i.e., 122. Now, find the smallest number from remaining numbers: 932, 952, 942. That is, 932. Find the smaller number from 952 and 942 i.e., 942.
The last number is the biggest: 952.
Therefore, 122, 932, 942, 952 are arranged in ascending order.
2. Arrange the numbers 113, 184, 838, 648 in descending order.
First find the biggest number i.e., 838. Now, find the biggest number from remaining numbers: 113, 184, 648. That is, 648.
Find out the bigger number from 113 and 184 i.e., 184.
The last number is the smallest: 113.
Therefore, 838, 648, 184, 113 are arranged in descending order.
Questions on Comparison of Three-digit Numbers:
I. Write the correct sign (>, < or =)
(i) 807 ............ 721
(ii) 87 ............ 40
(iii) 597 ............ 848
(iv) 927 ............ 498
(v) 759 ............ 216
(vi) 357 ............ 589
(vii) 444 ............ 444
(viii) 888 ............ 777
(ix) 256 ............ 572
(x) 201 ............ 602
(xi) 346 ............ 346
(xii) 652 ............ 352
II. Write in ascending order:
(i) 50, 20, 10, 40, 70, 60
(ii) 24, 18, 78, 64, 83, 55
(iii) 782, 364, 598, 528, 610, 798
(iv) 368, 316, 552, 225, 749, 493
(v) 537, 400, 163, 662, 225, 897
III. Write in descending order:
(i) 221, 631, 170, 492, 538, 113
(ii) 442, 113, 262, 552, 749, 821
(iii) 105, 90, 172, 450, 552, 339
(iv) 90, 420, 117, 768, 688, 180
(v) 172, 450, 680, 351, 536, 223
IV. Put <, > or = signs to compare the following numbers.
(i) 29 .............. 29
(ii) 24 .............. 204
(iii) 111 .............. 11
(iv) 55 .............. 555
(v) 204 .............. 214
(vi) 324 .............. 169
(vii) 673 .............. 149
(viii) 888 .............. 999
(ix) 213 .............. 231
V. Encircle the smallest number in the following sets.
(i) 638, 725, 857, 541
(ii) 413, 314, 431, 134
(iii) 201, 211, 111, 101
(iv) 232, 322, 223, 332, 233
VI. Encircle the greatest number in the following sets.
(a) 359, 673, 476, 299
(b) 735,573, 375, 537
(c) 20, 202, 222, 22
(d) 545, 554, 445, 454, 455
VII. Arrange the following numbers in ascending order.
(i) 165, 432, 245, 320
(ii) 825, 655, 890, 950
(iii) 580, 575, 543, 640
(iv) 200, 350, 105, 348
(v) 264, 295, 215, 279
(vi) 763, 768, 760, 764
VIII. Arrange the following numbers in descending order.
(i) 242, 282, 232, 211
(ii) 105, 108, 217, 215
(iii) 450, 970, 840, 320
(iv) 540, 980, 760, 580
(v) 847, 826, 890, 984
(vi) 461, 469, 460, 464
From Comparison of Three-digit Numbers to HOME PAGE
Didn't find what you were looking for? Or want to know more information about Math Only Math. Use this Google Search to find what you need.
Recent Articles
-
Quadrilaterals | Four Sided Polygon | Closed Figure | Adjoining Figure
Jul 14, 25 02:55 AM
Quadrilaterals are known as four sided polygon.What is a quadrilateral? A closed figure made of our line segments is called a quadrilateral. For example: -
Formation of Numbers | Smallest and Greatest Number| Number Formation
Jul 14, 25 01:53 AM
In formation of numbers we will learn the numbers having different numbers of digits. We know that: (i) Greatest number of one digit = 9, -
5th Grade Geometry Practice Test | Angle | Triangle | Circle |Free Ans
Jul 14, 25 01:53 AM
In 5th grade geometry practice test you will get different types of practice questions on lines, types of angle, triangles, properties of triangles, classification of triangles, construction of triang… -
5th Grade Circle Worksheet | Free Worksheet with Answer |Practice Math
Jul 11, 25 02:14 PM
In 5th Grade Circle Worksheet you will get different types of questions on parts of a circle, relation between radius and diameter, interior of a circle, exterior of a circle and construction of circl… -
Construction of a Circle | Working Rules | Step-by-step Explanation |
Jul 09, 25 01:29 AM
Construction of a Circle when the length of its Radius is given. Working Rules | Step I: Open the compass such that its pointer be put on initial point (i.e. O) of ruler / scale and the pencil-end be…
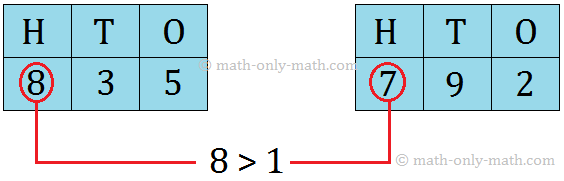








New! Comments
Have your say about what you just read! Leave me a comment in the box below. Ask a Question or Answer a Question.