Angle of Elevation

We have already learnt about trigonometry in previous units in detail. Trigonometry has its own applications in mathematics and in physics. One such application of trigonometry in mathematics is "height and distances". To know about height and distances, we have to start from the most basic part of that, which is "angle of elevation" and "angle of depression". The first and foremost angles that we are going to study about here is angle of elevation. In this part of height and distances we will be discussing about angle of elevation in detail.

Definition of Angle of Elevation:

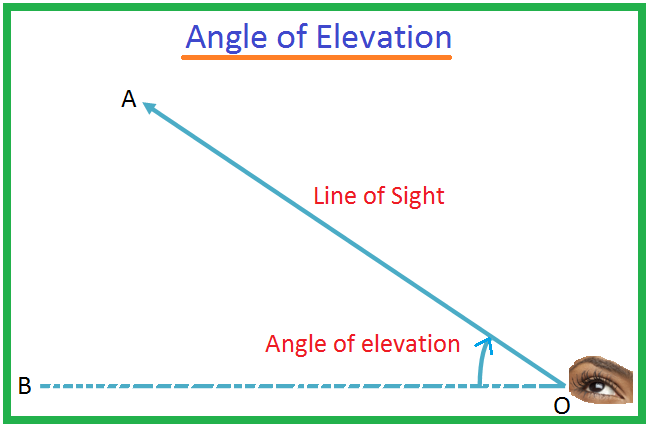
The angle of elevation of an object as seen by the observer is defined as the angle between the horizontal and the line from the object to the observer’s eye. The line in which observer’s eye is there is known as the line of sight.

Let O be the eye of an observer and A be an object above the level of the eye. The ray OA is called the line of sight. Let OB be the horizontal line through O. Then the angle AOB is called the angle of elevation of the object A as seen from O.

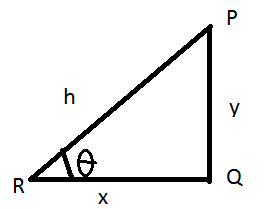
Let us assume an example where an observer is standing on the ground in front of a pole at a distance of ‘x’ meters from the bottom of the pole. Let us assume that height of pole is ‘y’ meters. If the observer is seeing the top most point of the pole from the ground level, and the angle made by the observer’s eye and the top most point of pole be ‘theta(ϴ)’ in the given figure:

In the above figure, let

P be the top most point of the pole.

Q be the bottom point of the pole.

R be the position of the observer’s eye.

Then,

PQ be the pole of height ‘y’ units;

QR be the distance between the bottom of pole and observer’s eye of ‘x’ units.

PR be the line of sight or the line along which observer is observing the top of the pole of ‘h’ units.

The angle ‘θ’ is the angle of elevation, and it can be found using following formulae:

sin θ = y/h; cosec θ = h/y

cos θ = x/h; sec θ = h/x

tan θ = y/x; cot θ = x/y.

depending upon the data given in the question, corresponding formula is applied to find out the angle of elevation.

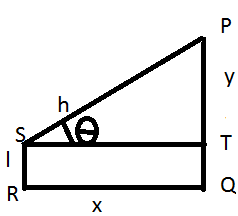
Another type of problem comes when the height of man is given in the question. Let us see how to solve that question:

Here SR is the height of man as ‘l’ units and height of pole to be considered will be (h - l) units. The line of sight in this case will be PS and angle of elevation will be ‘θ’. 

PQ = y, TQ = SR = l, PT = (y - l)

QR = ST = x, PS = h.

The formulae in this case will become:

          sin θ = (y - l)/h; cosec θ = h/(y - l)

          cos θ = x/h; sec θ = h/x

          tan θ = (y-  l)/x; cot θ = x/(y - l).

10th Grade Heights and Distances

Let us look at the following examples to see how to find out the angle of elevation:

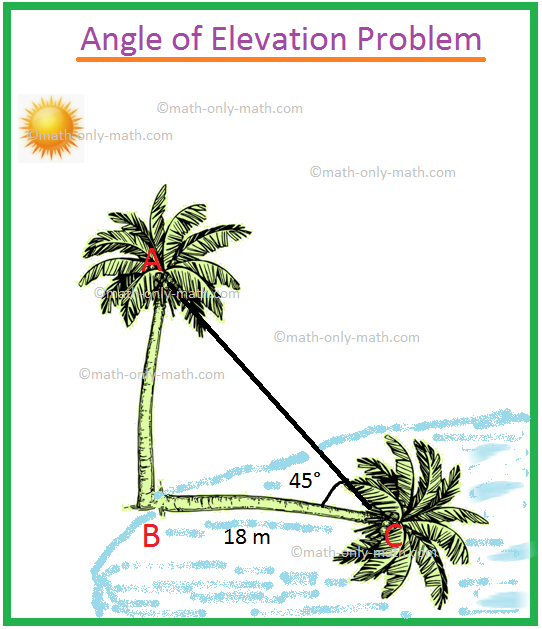
1. When angle of elevation of the Sum is 45°, the shadow of a coconut tree is 15 m in length. What is the height of the coconut tree?

Solution:

Let AB denote the height of the coconut tree and BC denote the length of the shadow.

Therefore, according to the problem ∠ACB = 45°, BC = 18 m.

Let the height of the coconut tree AB = x meters.

Now, tan 45° = \(\frac{AB}{BC}\)

     ⟹ \(\frac{AB}{BC}\) = tan 45°

     ⟹ \(\frac{x}{18}\) = 1

     ⟹ x = 1

Therefore, the height of the coconut tree is 18 meters.

2. The height of a pole is 30 m. A man is standing at a distance of 20 m from the foot of the pole. The man looks at the top most point of the point from the place where he is standing. Find out the angle made by the man’s eye with the top most point of the pole.

Solution:

The above problem can be visualized as:

From the given problem:

PQ = height of the pole = 30 m

QR = distance between the man and the foot of the pole = 20 m

We have to find angle ‘θ’ which the angle made by the man’s eye with the top most point of the pole and is angle of elevation.

We know that, tan θ = PQ/QR

⟹ tan θ = 30/20

⟹ θ = tan^-1 (30/20)

⟹ θ = tan^-1 (3/2)

⟹ θ = 56.3°.

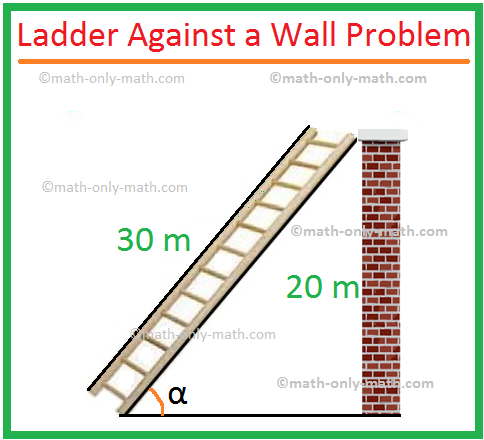
3. A ladder of length 30 m is kept in against a wall of length 20m such that their topmost point is in contact with one another and their bottom point are at certain distance as shown in the figure. Find the angle subtended by the ladder on the floor.

Solution:

The length of ladder is BA = 30 m

The height of wall is BC = 20 m

We have to find angle BAC = angle subtended by ladder on the floor.

Let angle BAC = α

We know that, 

sin α = BC/BA

⟹ sin α = 20/30

⟹ α = sin^-1 (20/30)

⟹ α = sin^-1 (2/3)

⟹ α = 41.81⁰.

4. A man is standing in front of a wall and looking at its topmost point. If the angle of elevation is 60°. If the height of wall is 40 m, then find the distance between the foot of the man and the wall.

Solution:

The given problem can be visualized as:

Here, angle of elevation, θ = 60^o

Height of wall, y = 40 m.

Distance between foot of man and the wall = x

We know that,

tan θ = y/x

⟹ tan θ = 40/x

⟹ x = 40/tan θ

⟹ x = 40/tan 60^o

⟹ x = 40/1.732

⟹ x = 23.09

Hence distance between foot of man and wall is 23.09 m or 23.1 m.

5. A man of height 1 m 30 cm is standing in front of a tree of height 30 m. find the angle of elevation to be made by the man’s eyes so as to look at the topmost point of the tree, if the man is standing at a distance of 5 m from the tree.

Solution:

The given problem can be visualized as:

Here, PQ is the height of tree = 30m

SR is the height of man = 1 m 30 cm = 1.30 m

RQ is the distance between the foot of the man and the tree = ST = 5 m

We have to find the angle of elevation, θ = ?

We know that,

     tan θ = (y - l)/x

⟹ tan θ = (30 - 1.30)/5

⟹ tan θ = 5.74

⟹ θ = tan^-1 (5.74)

⟹ θ = 80.117^o.

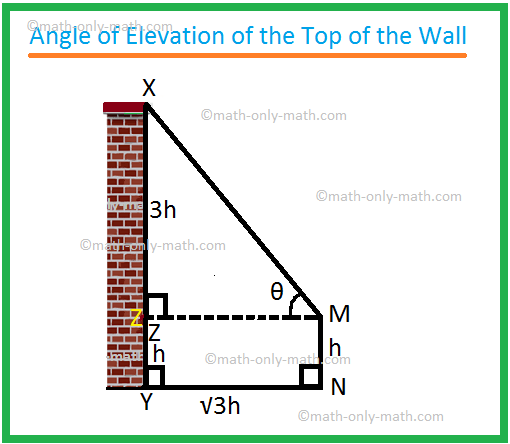
6. The height of an observer is h meters. He stands on a horizontal ground at a distance \(\sqrt{3}\)h metres from a vertical wall of height 4h metres. Find the angle of elevation of the top of the wall as seen by the observer. 

Solution:

Let MN be the observer and XY be the wall. 

Let MZ ⊥ XY. Here MN = h metres, XY = 4 h metres and YN = \(\sqrt{3}\)h metres.

Clearly, from geometry, YZ = MN = h metres

and MZ = NY = \(\sqrt{3}\)h metres.

Therefore, XZ = (4h - h) metres = 3 h metres.

In the right-angled triangle XZM,

                            tan ∠XZM = tan θ = \(\frac{XZ}{ZM}\)

                                          ⟹ tan θ = \(\frac{3h}{\sqrt{3}h}\)

                                          ⟹ tan θ = (\sqrt{3}\)

                                          ⟹ tan θ = tan 60°

                                          ⟹ θ = 60°

Therefore, required angle of elevation = 60°.

10th Grade Math

From Angle of Elevation to HOME