Worksheet on Heights and Distances

In worksheet on heights and distances we will practice different types of real life word problem trigonometrically using a right-angled triangle, angle of elevation and angle of depression.

1. A ladder rests against a vertical wall such that the top of the ladder reaches the top of the wall. The ladder is inclined at 60° with the ground, and the bottom of the ladder is 1.5 m away from the foot of the wall. Find

(i) the length of the ladder, and

(ii) the height of the wall.

2. An aeroplane takes off at an angle of 30° with the horizontal ground. Find the height of the aeroplane above the ground when it has travelled 184 m without changing direction.

3. The angle of elevation of the top of a vertical cliff from a point 15 m away from the foot of the cliff is 60°. Find the height of the cliff to the nearest metre.

4. The length of the shadow of a pillar is \(\frac{1}{\sqrt{3}}\) times the height of the pillar. Find the angle of elevation of the sun.

5. A ship is at a distance of 200 m from a tall tower. What is the angle of depression (to the nearest degree) of the ship found by a man after climbing 50 m up the tower?

6. The top of a tall vertical palm tree having been broken by the wind struck the ground at an angle of 60° at a distance of 9 m from the foot of the tree. Find the original height of the palm tree.

7. A 10-m-height pole is kept vertical by a steel wire. The wire is inclined at an angle of 40° with the horizontal ground. If the wire runs from the top of the pole to the point on the ground where its other end is fixed, find the length of the wire.

8. A tower is 64 m tall. A man standing erect at a distance of 36 m from the tower observes the angle of elevation of the top of the tower to be 60°. Find the height of the man.

9. From the top of a tall building of height 24 m, the angle of depression of the top of another building is 45° whose height is 10 m. Find the distance between the two buildings.

10. A tower stands by the side of a river at P. On the other side of the river, Q is a point on the bank such that PQ is the width of the river. R is the point on the bank of Q such that P, Q and R are in the same straight line. If QR = 5 metre and angles of elevation of top of the tower from Q area R are 60° and 45° respectively, find the width of the river and the height of the tower.

11. The angles of depression of two boats on a river from the top of a pole 30 metres high on the bank of the river are 60° and 75°. If the boats are in line with the pole, find the distance between the boats to the nearest metre.

12. A man standing on a cliff observes a ship at an angle of depression 30°, approaching the shore just beneath him. Three minutes later, the angle of depression of the ship is 60°. How soon will it reach the shore?

13. A man on the bank of a stream of observes a tree on the opposite bank exactly across the stream. He finds the angle of elevation of the top of the tree to be 45°. On receding perpendicularly a distance of 4 metre from the bank, he finds that the angle of elevation reduces by 15°. Is this information sufficient for the man to determine the height of the tree and the width of the stream? If so find them.

14. From the top of a light house the angles of depression of two ships on opposite sides of the light house were observed to be 60° and 45°. If the height of the light house is 100 m and the foot of the light house is in line with the ships, find the distance between the two ships.

15. From the top of a tower 40 m tall the angle of depression of the nearer of the two points P and Q on the ground on diametrically opposite sides of the tower is 45°. Find the angle of depression of the other point to the nearest degree if the distances of the two points from the base of the tower are in the ratio 1 : 2.

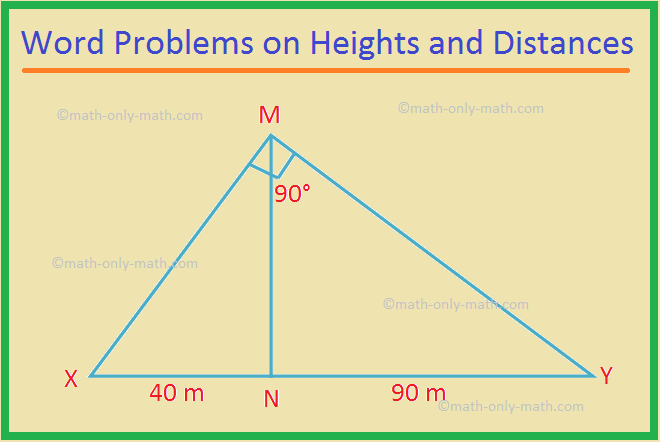
16. In the figure MN is a tower X and Y are two places on the ground on the either side of the tower such that XY subtends a right angle at M. If the distances of X and Y from the base N of the tower are 40 m and 90 m respectively. Find the height of the tower.

17. The angle of elevation of the top of an unfinished tower from a place at a distance of 50 m from the tower is 44° 40’. To what further height the unfinished tower should me raised so that the angle of elevation of the top of the tower from the same place would become 59° 30’?

18. A flagstaff, 5 m tall, stands on a vertical pole. The angles of elevation of the top and the bottom of the flagstaff from a point on the ground are found to be 60° and 30° respectively. Find the height of the pole.

19. A vertical pole fixed to the ground is divided into two parts by a mark on it. Each of the parts subtends an angle 30° at a place on the ground.

(i) Find the ratio of the two parts.

(ii) If the place on the ground is 15 m away from the base of the pole, find the lengths of the two parts of the pole.

20. A flagstaff is fixed on the top of mound and the angles of elevation of the top and the bottom of the flagstaff are 60° and 30° respectively at a point on the ground. Show that the length of the flagstaff is twice the height of the mound.

21. A man P walking towards a building AB finds that the building disappears from his view when the angle of elevation of the top C of a wall is x°, where tan x° = 1/3. The wall is 1.8 m high, and the distance between the wall and the building is 3.6 m. Find the height of the building.

22. A vertical tower subtends a right angle at the top of a vertical flag on the ground, the height of the flag being 10 m .If the distance between the tower and the flag be 20 m, find the height of the tower.

23. A vertical pole on one side of a street subtends a right angle at the top of a lamp post exactly on the opposite side of the street. If the angle of elevation of the top of the lamp post from the base of the pole is 58° 30’ and the width of the street is 30 m, find the heights of the pole and the lamp post.

24. From the top of a hill 200 m height, the angles of depression of the top and the bottom of a pillar are 45° and 59° 36’respectively. Find the height of the pillar and its distance from the hill.

25. A bird is perched on the top of a tree 20 m high and its angle of elevation from a point on the ground is 45°. The bird flies off horizontally straight away from the observer and in 1 sec the angle of elevation of the bird reduces to 35°. Find the speed of the bird.

26. The angles of depression and elevation of top of 12 m high wall from the top and the bottom of a tree are 60° and 30° respectively. Find

(i) the height of the tree, and

(ii) the distance of the tree from the wall.

27. Two pillars of equal height stand on either side of a road which is 40 m wide. From a point on the road between the pillars, the angles of elevation of tops of the pillars are 30° and 60°. Find

(i) the position of the point of the point on the road, and

(ii) the height of each pillar.

28. A ladder rests against a house on one side of a street. The angle of elevation of the top of the ladder is 60°. The ladder is turned over to rest against a house. On the other side of the street and the elevation now becomes 42° 50’. If the ladder is 40 m long, find the breadth of the street.

29. The angle of elevation of a cloud from a point h metre above a lake is 30° and the angle of depression of its reflection is 45°. If the height of the cloud be 200 metres, Find h.

30. A house, 15 metres high, stands on one side of a park and from a point on the roof of the house, the angle of depression of the foot of a chimney is 30° and the angle of elevation of the top of the chimney from the foot of the house is 60°. What is the height of the chimney? What is the distance between the house and the chimney?

Answers on worksheet on heights and distances are given below to check the exact answers of the questions. 

 Answers:

1. (i) 3 metres.

(ii) 2.6 metres.

2. 92 metres

3. 26 metres

4. 60°

5. 14°

6. 33.6 metres.

7. 15.6 metres.

8. 1.65 metres.

9. 14 metres.

10. 6.83 metres, 11.83 metres respectively.

11. 9 metres.

12. 4½ minutes after the first observation.

13. Yes; Each = 5.46 metres.

14. 157.74 metres.

15. 27°

16. 60 metres.

17. 35.47 metres.

18. 2.5 metres.

19. (i) Lower part : Upper part = 1 : 2

(ii) Lower part = 8.66 metres, upper part = 17.32 metres.

21. 3 metres.

22. 50 metres.

23. 67.34 metres, 48.96 metres respectively.

24. 82.2 metres, 117.8 metres.

25. 8.56 m/sec.

26. (i) 48 metres.

(ii) 20.78 metres.

27. (i) 10 metres and 30 metres from the pillars (two positions)

(ii) 17.32 metres.

28. 49.33 metres.

29. 53.6 metres.

30. 45 metres, 15√3 metres

10th Grade Math

From Worksheet on Heights and Distances to HOME PAGE