Sum of the Exterior Angles of an n-sided Polygon

Here we will discuss the theorem of the sum of all exterior angles of an n-sided polygon and sum related example problems.

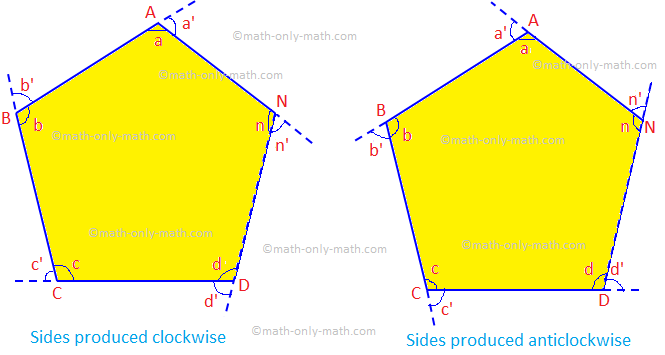
If the sides of a convex polygon are produced in the same order, the sum of all the exterior angles so formed is equal to four right angles.

Given: Let ABCD .... N be a convex polygon of n sides, whose sides have been produced in the same order.

To prove: The sum of the exterior angles is 4 right angles, i.e., ∠a’ + ∠b’ + ∠c’ + ..... + ∠n’ = 4 × 90° = 360°.

Proof:

Note:

1. In a regular polygon of n sides, each exterior angle = \(\frac{360°}{n}\).

2. If each exterior angle of a regular polygon is x°, the polygon has \(\frac{360}{x}\) sides.

3. The greater the number of sides of a regular polygon, the greater is the value of each interior angle and the smaller is the value of each exterior angle.

Solved examples on finding the sum of the interior angles of an n-sided polygon:

1. Find the measure of each exterior angle of a regular pentagon.

Solution:

Here, n = 5.

Each exterior angle = \(\frac{360°}{n}\)

                             = \(\frac{360°}{5}\)

                             = 72°

Therefore, the measure of each exterior angle of a regular pentagon is 72°.

2. Find the number of sides of a regular polygon if each of its exterior angles is (i) 30°, (ii) 14°.

Solution:

We know, total number of sides of a regular polygon is \(\frac{360}{x}\) where, each exterior angle is x°.

(i) Here, exterior angle x = 30°

Number of sides = \(\frac{360°}{30°}\)

                        = 12

Therefore, there are 12 sides of the regular polygon.

(ii) Here, exterior angle x = 14°

Number of sides = \(\frac{360°}{14°}\)

                        = 25\(\frac{5}{7}\), is not a natural number

Therefore, such a regular polygon does not exist.

3. Find the number of sides of a regular polygon if each of its interior angles is 160°.

Solution:

Each interior angle = 160°

Therefore, each exterior angle = 180° - 160° = 20°

We know, total number of sides of a regular polygon is \(\frac{360}{x}\) where, each exterior angle is x°.

Number of sides = \(\frac{360°}{20°}\) = 18

Therefore, there are 18 sides of a regular polygon.

4. Find the number of sides of a regular polygon if each interior angle is double the exterior angle.

Solution:

Let each exterior angle = x°

Therefore, each interior angle = 180° - x°

According to the problem, each interior angle is double the exterior angle i.e.,

180° - x° = 2x°

⟹ 180° = 3x°

⟹ x° = 60°

Therefore, the number of sides = \(\frac{360}{x}\)

                                             = \(\frac{360}{60}\)

                                             = 6

Therefore, there are 6 sides of a regular polygon when each interior angle is double the exterior angle.

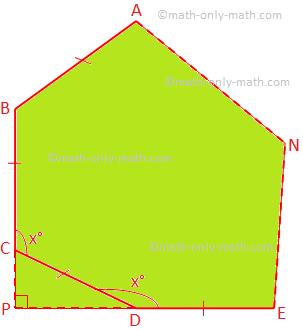
5. Two alternate sides of a regular polygon, when produced, meet at right angles. Find:

(i) each exterior angle of the polygon,

(ii) the number of sides of the polygon

Solution:

(i) Let ABCD ...... N be a regular polygon of n sides and each interior angle = x°

According to the problem, ∠CPD = 90°

∠PCD = ∠PDC = 180° - x°

Therefore, from ∆CPD,

180° - x° + 180° - x° + 90° = 180°

⟹ 2x° = 270°

⟹ x° = 135°

Therefore, each exterior angle of the polygon = 180° - 135° = 45°.

(ii) Number of sides = \(\frac{360°}{45°}\) = 8.

6. There are two regular polygons with number of sides equal to (n – 1) and (n + 2). Their exterior angles differ by 6°. Find the value of n.

Solution:

Each exterior angle of the first polygon = \(\frac{360°}{ n – 1}\).

Each exterior angle of the second polygon = \(\frac{360°}{ n + 2}\).

According to the problem, each exterior angle of the first polygon and the second polygon differs by 6° i.e., \(\frac{360°}{ n – 1}\) - \(\frac{360°}{ n + 2}\).

⟹ 360° (\(\frac{1}{ n – 1}\) - \(\frac{1}{ n + 2}\)) = 6°

⟹ \(\frac{1}{ n – 1}\) - \(\frac{1}{ n + 2}\) = \(\frac{6°}{360°}\)

⟹ \(\frac{(n + 2) – (n – 1)}{(n – 1)(n + 2)}\) = \(\frac{1}{60}\)

⟹ \(\frac{3}{n^{2} + n - 2}\) = \(\frac{1}{60}\)

⟹ n\(^{2}\) + n – 2 = 180

⟹ n\(^{2}\) + n – 182 = 0

 ⟹ n\(^{2}\) + 14n – 13n – 182 = 0

⟹ n(n + 14) – 13(n + 14) = 0

⟹ (n + 14)(n - 13) = 0

Therefore, n = 13 (since n ≠ -14).

9th Grade Math

From Sum of the Exterior Angles of an n-sided Polygon to HOME PAGE