Smaller Units to Bigger Units

To convert a smaller unit into a bigger unit, we move the decimal point to the left. In other words, we can say that we divide.

This is very important for us to learn how to convert smaller units into bigger units. We use it often in our daily life.

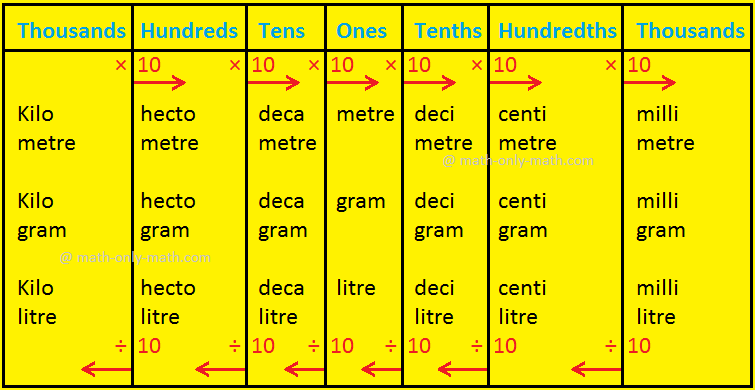
Measurement of length, mass and capacity tables can be represented in the form of a place-value chart as shown below.

Converting Smaller Units of Length into Bigger Units of Length:

For Example:

1. Convert 80 mm into cm.

Solution:

We know that 10 mm = 1 cm

                        80 mm = $\frac{80}{10}$ cm

                                   = 8 cm

2. Convert 485 mm into cm.

Solution:

485 mm = 480 mm + 5 mm

We know that 10 mm = 1 cm

480 mm + 5 mm = $\frac{480}{10}$ cm + 5 mm

                          = 48 cm 5 mm

3. Convert 15000 m into km.

Solution:

We know that 1000 m = 1 km

So, 15000 m = $\frac{15000}{1000}$ km

                    = 15 km

3. Convert 577 centimetres to decametres

1000 cm = 1 dam

577 cm = (577 ÷ 1000) dam

577 cm = 0.577 dam

Converting Smaller Units of Mass into Bigger Units of Mass:

To convert lower units of mass to higher units, we multiply by 1000. A quick way to convert is to write three digits from right as lower unit and the remaining as higher unit.

For example:

1. Convert 14000 mg into g.

We know that 1000 mg = 1 g

So, 14000 mg = $\frac{14000}{1000}$ g

                     = 14 g 

2. Express 3180 g as kg.

3180 g = 3000 g + 180 g

           = $\frac{3000}{1000}$ kg + 180 g

           = 3 kg 180 g

3. Convert 7000 grams to kilograms.

1000 g = 1 kg

7000 g = (7000 ÷ 1000) kg

7000 g = 7 kg

4. Convert 225 kilograms to quintals

100 kg = 1 quintal

225 kg = (225 ÷ 100) quintals

225 kg = 2.25 quintals

5. Convert 36 quintals to tonnes

10 quintals = 1 tonne

36 quintals = (36 ÷ 10) tonnes

36 quintals = 3.6 tonnes

6. Convert 415 kilograms to tonnes

1000 kg = 1 tonne

415 kg = (415 ÷ 1000) tonnes

415 kg = 0.415 tonnes

Converting Smaller Units Capacity into Bigger Units Capacity:

To convert milliliters into liters, we divide the number of milliliters (ml) by 1000. A quick way to convert ml into l is to write three digits from right as ml and the remaining as l.

For example:

1. Convert 76489 ml into l.

76489 ml = 76000 ml + 489 ml

                  = $\frac{76000}{1000}$ + + 489 ml

                  = 76 l 489 ml

2. Convert 375 litres to kilolitres.

1000 l = 1 kl

375 l = (375 ÷ 1000) kl

375 l = 0.375 kl

Alternate Method:

Conversion of Lower Units to Higher Units:

When a lowers unit is changed into a higher unit we divide the number of the lowers unit by the number showing the relationship between the two units.

For example:

1. 5728 g = 5000 g 728 g 5728 g = 5 kg 728 g 5728 g = 5.728 g

Also 5728 g = 5000 g + 700 g + 20 g + 8 g

                  = 5 kg 7 hg 2 dag 8 g

2. 328 cm = 300 cm + 28 cm 328 cm = 3 m 28 cm 328 cm = 3.28 m

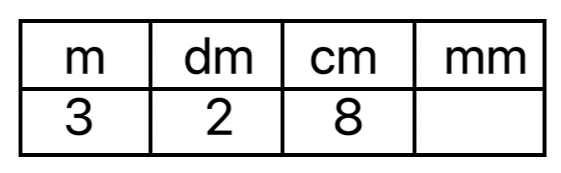
Also 328 cm = 300 cm + 20 cm + 8 cm

                  = 3 m 2 dm 8 cm

Solved examples for the conversion of smaller units to bigger units:

1. Convert 9362.8 grams into the following units.

(i) Decagrams

(ii) hectograms

(iii) kilograms

Solution:

Because 1 dag = 10 g

So, 1 g = $\frac{1}{10}$ dag

So, 9362.8 g = $\frac{9362.8}{10}$ = (9362.8 ÷ 10) dag = 936.28 dag

Thus,

(i) 9362.8 g = = (9362.8 ÷ 10) dag = 936.28 dag

(ii) 9362.8 g = = (9362.8 ÷ 100) hg = 93.628 hg, (Because 1 g = $\frac{1}{100}$ hg)

(ii) 9362.8 g = = (9362.8 ÷ 1000) kg = 9.3628 kg, (Because 1 g = $\frac{1}{1000}$ kg)

2. Convert 2345 millimetres into the following units.

(i) centimetres

(ii) metres

(iii) kilometres

Solution:

(i) 2345 millimetres = (2345 ÷ 10) = 234.5 centimetres, [Because 1 mm = $\frac{1}{10}$ cm]

(ii) 2345 millimetres = (2345 ÷ 1000) = 2.345 metres, [Because 1 mm = $\frac{1}{1000}$ m]

(iii) 2345 millimetres = (2345 ÷ 1000000) = 0.002345 kilometres, [Because 1 mm = $\frac{1}{1000000}$ km]

Let us consider another example involving different types of conversions.

3. Convert the following:

(i) 3598 mm to m

(ii) 4683254 mg to dg

(iii) 5923 ml to cl

Solution:

(i) 3598 mm

= (3598 ÷ 1000) m, [Because 1 mm = $\frac{1}{1000}$ m]

= 3.598 m

(ii) 4683254 mg

= (4683254 ÷ 100) dg, [Because 1 mg = $\frac{1}{100}$ dg]

= 46832.54 dg

(iii) 5923 ml

= (5923 ÷ 10) cl, [Because 1 ml = $\frac{1}{10}$ cl]

= 592.3 cl

4. Convert 12500 m into km.

Solution:

We know that 1000 m = 1 km

12500 m = 12000 m + 500 m

              = $\frac{12000}{1000}$ km + 500 m

              = 12 km 500 m

Questions and Answers on Smaller Units to Bigger Units:

I. Convert the given lengths:

(i) 40 mm = ………….. cm

(ii) 540 cm = ………….. m ………….. cm

(iii) 160 mm = ………….. cm

(iv) 1250 m = ………….. km ………….. m

(v) 10500 cm = ………….. m

(vi) 3500 cm = ………….. m ………….. cm

(vii) 612 cm = ………….. m ………….. cm

(viii) 41752 m = ………….. km ………….. m

Answers:

I. (i) 4 cm

(ii) 5 m 40 cm

(iii) 16 cm

(iv) 1 km 250 m

(v) 105 m

(vi) 35 m 0 cm

(vii) 6 m 12 cm

(viii) 41 km 752 m

4th Grade Math Activities

From Smaller Units to Bigger Units to HOME PAGE