Long Division Method with Regrouping and with Remainder

We will discuss here how to solve step-by-step the long division method with regrouping and with remainder.

Consider the following examples:

1. 527 ÷ 3

Division with Regrouping and with Remainder

Step I: Begin with hundreds digit

5 hundreds ÷ 3 = 1 hundred

with remainder 2 hundreds

Step II: Bring down 2 tens to the right of 2 hundreds

2 hundreds + 2 tens = 22 tens

Step III: 22 tens ÷ 3 = 7 tens with remainder 1 ten

Step IV: Bring down 7 ones to the right of 1 ten. Then,

1 ten + 7 ones = 17 ones

Step V: 17 ones ÷ 3 = 5 ones with remainder 2 ones.

Therefore, 527 ÷ 3 = 175 with remainder 2


2. 6311 ÷ 4

Long Division Method with Regrouping and with Remainder

Step I: Begin with thousands digit

6 thousands ÷ 4 = 1 thousand with remainder 2 thousands

Step II: Bring down 3 hundreds to the right of 2 thousands. Then,

2 thousands + 3 hundreds = 23 hundreds

Step III: Now 23 hundreds ÷ 4 = 5 hundreds with remainder 3 hundreds

Step IV: Bring down 1 ten to the right of 3 hundreds

Then, 3 hundreds + 1 ten = 31 tens

Step V: Now, 31 tens ÷ 4 = 7 tens with remainder 3 tens

Step VI: Bring down 1 one to the right of 3 tens

then 3 tens + 1 one = 31 ones

Now 31 ones ÷ 4 = 7 ones with remainder 3 ones

Therefore 6311 ÷ 4 = 1577 with remainder 3








3rd Grade Math Worksheets

3rd Grade Math Lessons

From Long Division Method with Regrouping and with Remainder to HOME PAGE



Didn't find what you were looking for? Or want to know more information about Math Only Math. Use this Google Search to find what you need.



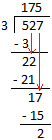
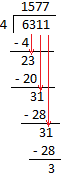
New! Comments

Have your say about what you just read! Leave me a comment in the box below. Ask a Question or Answer a Question.

Share this page: What’s this?

Recent Articles

RSS

  1. Word Problems on Area and Perimeter | Free Worksheet with Answers

    Jul 26, 24 04:58 PM

    word problems on area and perimeter

    Read More

  2. Worksheet on Perimeter | Perimeter of Squares and Rectangle | Answers

    Jul 26, 24 04:37 PM

    Most and Least Perimeter
    Practice the questions given in the worksheet on perimeter. The questions are based on finding the perimeter of the triangle, perimeter of the square, perimeter of rectangle and word problems. I. Find…

    Read More

  3. Perimeter and Area of Irregular Figures | Solved Example Problems

    Jul 26, 24 02:20 PM

    Perimeter of Irregular Figures
    Here we will get the ideas how to solve the problems on finding the perimeter and area of irregular figures. The figure PQRSTU is a hexagon. PS is a diagonal and QY, RO, TX and UZ are the respective d…

    Read More

  4. Perimeter and Area of Plane Figures | Definition of Perimeter and Area

    Jul 26, 24 11:50 AM

    Perimeter of a Triangle
    A plane figure is made of line segments or arcs of curves in a plane. It is a closed figure if the figure begins and ends at the same point. We are familiar with plane figures like squares, rectangles…

    Read More

  5. 5th Grade Math Problems | Table of Contents | Worksheets |Free Answers

    Jul 26, 24 01:35 AM

    In 5th grade math problems you will get all types of examples on different topics along with the solutions. Keeping in mind the mental level of child in Grade 5, every efforts has been made to introdu…

    Read More