Hollow Cylinder

We will discuss here about the volume and surface area of Hollow Cylinder.

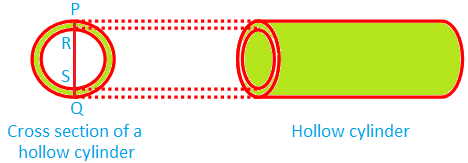
The above figure is showing a hollow cylinder and its cross section. 

A cross section of it perpendicular to the length (or height) is the portion bounded by two concentric circles.

Here, AB is the outer diameter and CD is the inner diameter of the circular cross section. AC (or BD) is the thickness of the material of which the hollow cylinder is made.

If R, r are the outer and inner radii respectively and t is the thickness then R = r + t, r = R - t, t = R - r.

The volume of the material = π(R² - r²) × Height.

The inner curved surface area = 2πr × Height, the outer curved surface area = 2πR × Height.

Solved Examples on Hollow Cylinder:

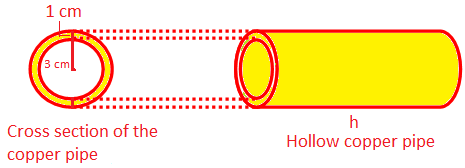
A hollow copper pipe of inner radius 3 cm and outer radius 4 cm is melted and changed into a solid right circular cylinder of the same length as that of the pipe. Find the area of the cross section of the solid cylinder.

Solution: 

The area of the cross of the pipe = (π ∙ 4² - π ∙ 3²) cm² = 7π cm²

Therefore, the volume of the pipe = (Area of the cross section) × length

                                                 = 7π × h cm³;

                                                       (Taking length of the pipe = h cm)

                                                 = 7πh cm³.

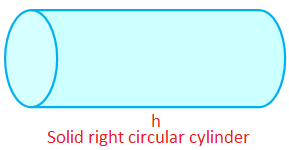
The volume of the right circular cylinder = πr²h cm³.

                 (Taking the radius of the cross section of the cylinder = r cm)

According to the question, these two volumes are equal.

Therefore, 7πh cm³ = πr²h cm³

                     ⟹ r² = 7.

Therefore, the area of the cross section of the sold cylinder

                                                                  = πr² cm²

                                                                  = \(\frac{22}{7}\) ∙ 7 cm²

                                                                  = 22 cm².

9th Grade Math

From Hollow Cylinder to HOME PAGE