Enlargement Transformation

We will discuss here about the similarity on enlargement transformation.

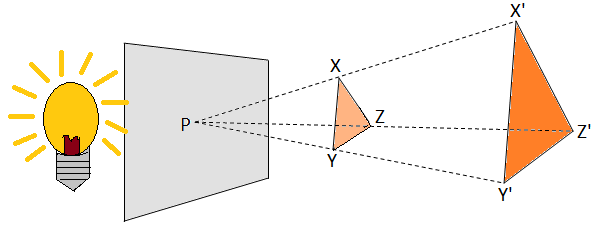
Cut out some geometrical figures like triangles, quadrilaterals, etc., from a piece of cardboard. Now we will hold these figures, one-by-one, between a point source of light and a wall. Then look at the shadow cast by each figure on the wall. The shadows have the same shapes as the original figures, but are larger in size. The shadows are said to be similar to the original figures.

In the above figure, XYZ is a triangle and its shadow is ∆X’Y’Z’. 

By actual measurements it can be seen that ∠X = ∠X’, ∠Y = ∠Y’ and ∠Z = ∠Z’.

Thus, the two triangles are equiangular. Also, the shadow X’Y’Z’ is an enlarged image of the object XYZ. If the side X’Y’ = k × XY, the other sides are also enlarged in the same proportion,

i.e., Y’Z’ = k × YZ and Z’X’ = k × ZX.

Here k is said to be the enlargement factor and $\frac{X’Y’}{XY}$ = $\frac{Y’Z’}{YZ}$ = $\frac{Z’X’}{ZX}$ = k.

The point P is known as the centre of enlargement.

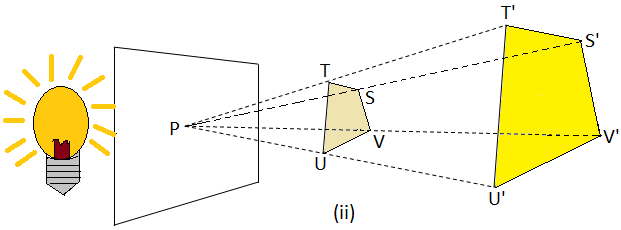
Similarly, in the figure below, the quadrilateral S’T’U’V’ is the enlarged image of the quadrilateral STUV. 

Here also, ∠S = ∠S’, ∠T = ∠T’, ∠U = ∠U’ and ∠V = ∠V’. If the enlargement factor m, we get $\frac{S’T’}{ST}$ = $\frac{T’U’}{TU}$ = $\frac{U’V’}{UV}$ = $\frac{V’S’}{VS}$ = m.

Solved Examples on Enlargement Transformation

1. A triangle XYZ has been enlarged by a scale factor 3 to a triangle X’ Y’ Z’. Find the length of:

(i) X’ Y’ if XY = 4 cm,

(ii) YZ if Y’ Z’ = 7.5 cm.

Solution:

Let $\frac{X’ Y’}{XY}$ = $\frac{Y’ Z’}{YZ}$ = $\frac{Z’ X’}{ZX}$ = k.

(i) $\frac{X’ Y’}{XY}$ = k.

⟹ $\frac{X’ Y’}{4 cm}$ = 3

⟹ X’ Y’ = 3 × 4

⟹ X’ Y’ = 12

(ii) $\frac{ Y’ Z’}{YZ}$ = k.

⟹ $\frac{7.5}{YZ}$ = 3

⟹ YZ = $\frac{7.5 cm}{3}$

⟹ YZ = 2.5 cm

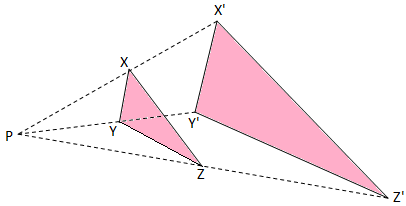
2. A triangle XYZ has been enlarged to ∆ X’Y’Z’ about the centre of enlargement O by a scale factor 2.5.

Find:

(i) X’Y’ if XY = 4 cm,

(ii) XZ if X’Z’ = 15 cm,

(iii) OX’ and XX’ if OX = 3 cm.

Solution:

(i) $\frac{X’Y’}{XY}$ = k.

⟹ $\frac{X’Y’}{4 cm}$ = 2.5

⟹ X’Y’ = 4 × 2.5 cm

⟹ X’Y’ = 10 cm

(ii) $\frac{X’Z’}{XZ}$ = k.

⟹ $\frac{15 cm}{XZ}$ = 2.5

⟹ XZ = $\frac{15 cm}{2.5}$

⟹ XZ = 6 cm

(iii) $\frac{OX’}{OX}$ = k.

⟹ $\frac{OX’}{3 cm}$ = 2.5

⟹ OX’ = 3 × 2.5 cm

⟹ OX’ = 7.5 cm

XX’ = OX’ - OX = 7.5 cm - 3 cm = 4.5 cm

9th Grade Math

From Enlargement Transformation to HOME PAGE