Subscribe to our ▶️ YouTube channel 🔴 for the latest videos, updates, and tips.
Dividend, Divisor, Quotient and Remainder
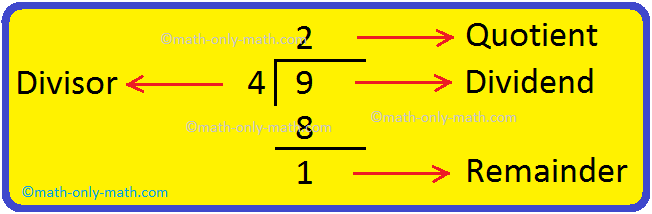
In division we will see the relationship between the dividend, divisor, quotient and remainder. The number which we divide is called the dividend. The number by which we divide is called the divisor. The result obtained is called the quotient. The number left over is called the remainder.
55 ÷ 9 = 6 and 1
Dividend Divisor Quotient Remainder
For example:
(i) Divide 217 by 4
(ii) Divide 5679 by 7
Remainder, 55 ÷ 9 can also write as 9) 55 ( or 9) 55Note: dividend = divisor × quotient + remainder
Understanding Remainder:
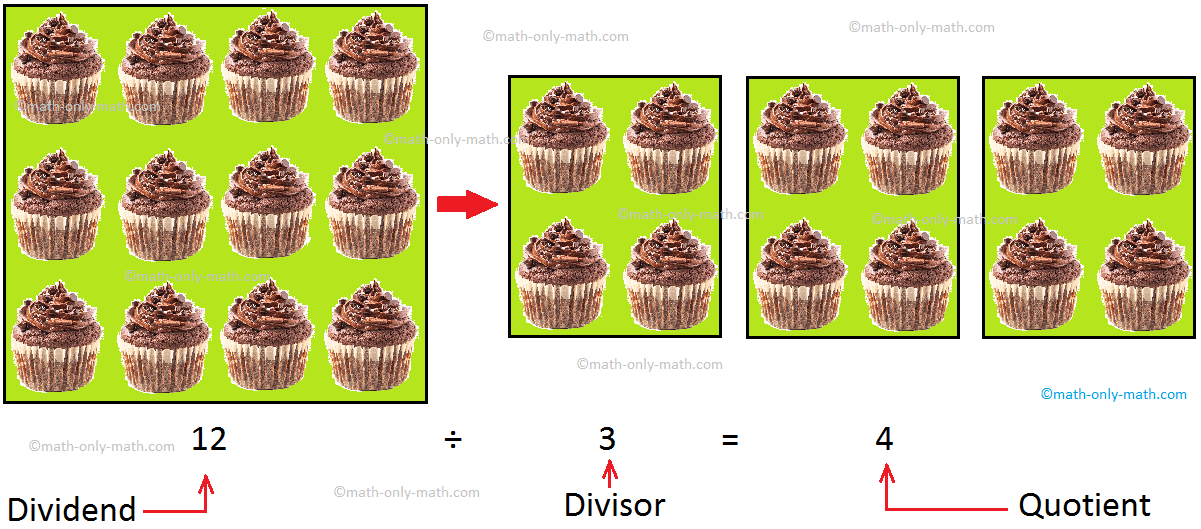
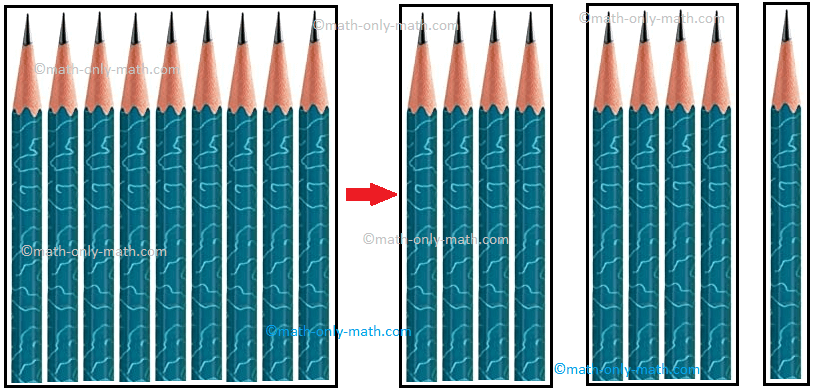
We know divisor means to split a large group of objects into small equal groups. The large group is called the dividend. The number of smaller equal groups is called the divisor and the number of objects in each smaller group is called the quotient.
Let us Divide 12 cupcakes among 3 children.
Now, let us Divide 9 pencils into 2 equal groups.
When we cannot make equal groups or share equally all the objects, the number which is left undivided is called the remainder. Remainder is always less than the divisor.
So, Dividend = Divisor × Quotient + Remainder
In the above example = 9 × 2 + 1
The dividend, divisor, quotient and remainder will help us to verify the answer of division. Add remainder (if any) with the product of divisor and quotient. The sum we get should be equal to the dividend.
Let us consider some examples to verify the answer of division.
1. Divide 38468 by 17 and verify the answer.
|
Now let us verify the answer; dividend = divisor × quotient + remainder 38468 = 17 × 2262 + 14 = 38454 + 14 = 38468 So, the answer is correct. |
The quotient is 2262 and the remainder is 14.
2. Divide 58791 by 36 and verify the answer.
|
Now let us verify the answer; dividend = divisor × quotient + remainder 58791 = 36 × 1633 + 3 = 58788 + 3 = 58791 So, the answer is correct. |
The quotient is 1633 and the remainder is 3.
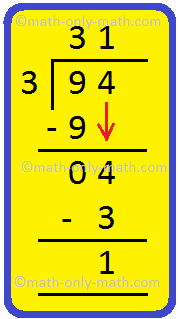
3. Divide 94 by 3 and verify the answer.
|
Step I: Write 94 inside the bracket and 3 on the left side of the bracket. Step II: Start division from left to right, Divide 9 tens by 3. We know that 3 × 3 = 9 Write 3 in the quotient and 9 below 9. Subtract 9 from 9. Step III: Bring down 4 from ones place. 3 goes into 4, 1 time and gives 1 as remainder. Write 1 in the quotient and subtract 3 from 4. |
Thus, quotient = 31 and remainder = 1 |
Check: To check answer, we use the following relationship:
Dividend = Divisor × Quotient + Remainder
94 = 3 × 31 + 1
94 = 93 + 1
94 = 94
Hence, division is correct.
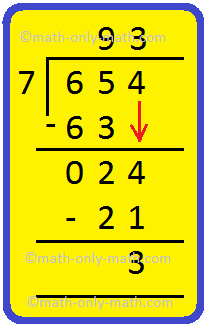
4. Divide 654 by 7 and verify the answer.
|
Step I: Write 654 inside the bracket and 7 on the left side of the bracket. Step II: The divisor 7 is greater than 6. So, consider first two digits 65. 7 goes into 65, 9 times and gives 2 as remainder. Step III: 24 is the new dividend. 7 goes into 24, 3 times and gives 3 as remainder. Write the quotient 3 and subtract 321 from 24. |
Thus, quotient = 93 and remainder = 3 |
Check: To check answer, we use the following relationship:
Dividend = Divisor × Quotient + Remainder
654 = 7 × 93 + 3
654 = 651 + 3
654 = 654
Hence, division is correct.
Therefore, to check a division sum, add the remainder to help product of divisor and quotient. The result should be equal to the dividend.
Properties
of division:
When zero is divided by a number the quotient is zero.
For example:
(i) 0 ÷ 4 = 0
(ii) 0 ÷ 12 = 0
(iii) 0 ÷ 25 = 0
(iv) 0 ÷ 314 = 0
(v) 0 ÷ 225 = 0
(vi) 0 ÷ 7135 = 0
Division of a number by zero is not possible.
For example, we cannot divide 74 by 0.
If we divide any number by 1, the quotient is the number itself.
For example:
(i) 28 ÷ 1 = 28
(ii) 4558 ÷ 1 = 4558
(iii) 335 ÷ 1 = 335
(iv) 9387 ÷ 1 = 9387
If we divide a non-zero number by itself, the quotient is 1.
For example:
(i) 45 ÷ 45 = 1
(ii) 98 ÷ 98 = 1
(iii) 1371 ÷ 1371 = 1
(iv) 5138 ÷ 5138 = 1
From Dividend, Divisor, Quotient and Remainder to HOME PAGE
Didn't find what you were looking for? Or want to know more information about Math Only Math. Use this Google Search to find what you need.
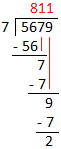
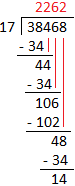
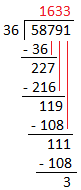


New! Comments
Have your say about what you just read! Leave me a comment in the box below. Ask a Question or Answer a Question.