Area and Perimeter of Combined Figures

Here we will solve different types of problems on finding the area and perimeter of combined figures.

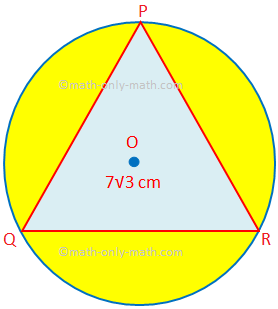
1. Find the area of the shaded region in which PQR is an equilateral triangle of side 7√3 cm. O is the centre of the circle.

 (Use π = \(\frac{22}{7}\) and √3 = 1.732.)

Solution:

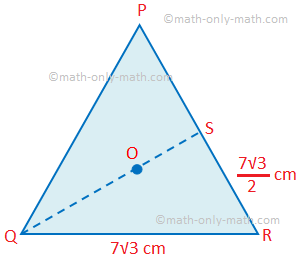
The centre O of the circle is the circumcentre of the equilateral triangle PQR. 

So, O is also the centroid of the equilateral triangle and QS ⊥ PR, OQ = 2OS. If the radius of the circle be r cm then

OQ = r cm,

OS = \(\frac{r}{2}\) cm,

RS = \(\frac{1}{2}\) PR = \(\frac{7√3}{2}\) cm

Therefore, QS\(^{2}\) = QR\(^{2}\) - RS\(^{2}\)

or, (\(\frac{3r}{2}\))\(^{2}\) = (7√3)\(^{2}\) - (\(\frac{7√3}{2}\))\(^{2}\)

or, \(\frac{9}{4}\) r\(^{2}\) = (1 - \(\frac{1}{4}\)) (7√3)\(^{2}\)

or, \(\frac{9}{4}\) r\(^{2}\) = \(\frac{3}{4}\) × 49 × 3

or, r\(^{2}\) = \(\frac{3}{4}\) × 49 × 3 × \(\frac{4}{9}\)

or, r\(^{2}\) = 49

Therefore, r = 7

Therefore, area of the shaded region = Area of the circle – Area of the equilateral triangle

                                                      = πr\(^{2}\) - \(\frac{√3}{4}\) a\(^{2}\)

                                                      = \(\frac{22}{7}\) × 7\(^{2}\) cm\(^{2}\) - \(\frac{√3}{4}\) × (7√3)\(^{2}\) cm\(^{2}\) 

                                                      = (154 - \(\frac{√3}{4}\) × 147) cm\(^{2}\)

                                                      = (154 - \(\frac{1.732 × 147}{4}\)) cm\(^{2}\)

                                                      = (154 - \(\frac{254.604}{4}\)) cm\(^{2}\)

                                                      = (154 - 63.651) cm\(^{2}\)

                                                      = 90349 cm\(^{2}\)

2. The radius of the wheels of a car is 35 cm. The car takes 1 hour to cover 66 km. Find the number of revolutions that a wheel of the car makes in one minute. (Use π = \(\frac{22}{7}\).)

Solution:

According to the problem, radius of a wheel = 35 cm.

The perimeter of a wheel = 2πr

                                     = 2 × \(\frac{22}{7}\) × 35 cm

                                     = 220 cm

Therefore, the number of revolutions of a wheel to cover 66 km = \(\frac{66 km}{220 km}\)

                                          = \(\frac{66 × 1000 × 100 cm}{220 cm}\)

                                          = \(\frac{3 × 1000 × 100}{10}\)

                                          = 30000

Therefore, the number of revolutions of a wheel to make in

                                                                 one minute = \(\frac{30000}{60}\)

                                                                                  = 500

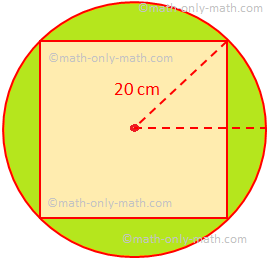
3. A circular piece of paper of radius 20 cm is trimmed into the shape of the biggest possible square. Find the area of the paper cut off. (Use π = \(\frac{22}{7}\).)

Solution:

The area of the piece of paper = πr\(^{2}\)

                                            = \(\frac{22}{7}\) × 20\(^{2}\) cm\(^{2}\)

If the side of the inscribed square be x cm then

20\(^{2}\) = (\(\frac{x}{2}\))\(^{2}\) + (\(\frac{x}{2}\))\(^{2}\)

or, 400 = \(\frac{1}{2}\) x\(^{2}\)

or, x\(^{2}\) = 800.

Therefore, the area of the paper cut off = The area of the circle - The area of the square

                                                          = πr\(^{2}\) - x\(^{2}\)

                                                          = \(\frac{22}{7}\) × 20\(^{2}\) cm\(^{2}\) - 800 cm\(^{2}\)

                                                          = (\(\frac{8800}{7}\) - 800) cm\(^{2}\)

                                                          = \(\frac{3200}{7}\) cm\(^{2}\)

                                                          = 457\(\frac{1}{7}\) cm\(^{2}\)

9th Grade Math

From Area and Perimeter of Combined Figures to HOME PAGE