6th Grade Algebra Worksheet

In 6th Grade Algebra Worksheet you will get different types of questions on basic concept of algebra, questions on number pattern, dot pattern, number sequence pattern, pattern from matchsticks, concept of variables, basic concept of algebraic expressions, types of algebraic expressions, problems on like terms and unlike terms, algebraic expressions using variables, application of algebraic expressions, how to find the solution of an equation and different type of word problems related to algebra.

1. Multiple Choice Questions (MCQ) on 6th Grade Algebra:

   Tick (✔) the correct option.

(i) Considering the sequence 6, 11, 16, 21, 26......... its n^th term is

(a) 5n

(b) 5n + 2

(c) 5n + 1

(d) (51 - 1)

(ii) The pattern to form 'U' through matchsticks is

(a) 2x

(b) x

(c) 4x

(d) 3x

(iii) In - 3p, the literal factor is

(a) 1

(b)-3

(c) p

(d) 0

(iv) In x⁸ the exponent is

(a) 8

(b) x

(c) 1

(d) 10

(v) The polynomial (2xy - 9) is

(a) monomial

(b) binomial

(c) trinomial

(d) multinomial

(vi) I think of a number x, subtract 3 from it and then divide by 5. The correct algebraic expression is

(a) 3 - x + 5

(b) x - \(\frac{3}{5}\)

(c) \(\frac{x - 3}{5}\)

(d) \(\frac{x}{5}\) - 3

(vii) Algebraic expression for the statement '5 times a number y taken away from 17' is

(a) 5y - 17

(b) 17-5y

(c) \(\frac{y}{5}\) - 17

(d) \(\frac{y}{5}\) + 17

(viii) If the marks obtained by a student in a mathematics test is 8 more than two-thirds of x, then its algebraic expression is.

(a) \(\frac{2}{3}\)x

(b) 8 - \(\frac{2}{3}\)x

(c) 8 + \(\frac{2}{3}\)x

(d) \(\frac{2}{3}\)x - 8

(ix) \(\frac{y}{4}\) - \(\frac{1}{2}\) = \(\frac{y}{3}\) + 1 then the value of y is

(a) 18

(b) -18

(c) 10

(d) 16

(x) \(\frac{1}{2}\)p + 1 = \(\frac{3}{2}\)p + 2 then the value of p is

(a) 1

(b) -1

(c) \(\frac{1}{2}\)

(d) - \(\frac{1}{2}\)

(xi) The value of x in 3x + 2 = 5

(a) 1

(b) 2

(c) 0

(d) \(\frac{7}{3}\)

(xii) Which of the following is not an equation?

(a) 2x - 2 = 0

(b) x - \(\frac{5}{2}\) = 3

(c) 5x - \(\frac{3}{2}\) = 2

(d) x - 2 < 5

(xiii) The solution of 5x - 23 = - 8 is

(a) x = - 3

(b) x = 3

(c) x = 4

(d) x = - 4

(xiv) On solving an equation we get 2x - \(\frac{1}{2}\) = - 5

(a) x = \(\frac{9}{2}\)

(b) x = - \(\frac{9}{2}\)

(c) x = \(\frac{9}{4}\)

(d) x = - \(\frac{9}{4}\)

(xv) If 12x - 8 = - 152 the value of x is

(a) 10

(b) -10

(c) 12

(d) -12

(xvi) If 5 less than the four-fifths of a number is 47, then the number is

(a) 60

(b) 65

(c) 50

(d) 55

Answer:

1. (i) → (c) 5n + 1

(ii) → (a) 2n

(iii) → (c) p

(iv) → (a) 8

(v) → (b) binomial

(vi) → (c) \(\frac{x - 3}{5}\)

(vii) → (b) 17 - 5y

(viii) → (c) 8 + \(\frac{2}{3}\)x

(ix) → (b) -18

(x) → (b) -1

(xi) → (a) 1

(xii) → (d) x - 2 < 5

(xiii) → (b) x = 3

(xiv) → (d) x = - \(\frac{9}{4}\)

(xv) → (d) -12

(xvi) → (b) 65

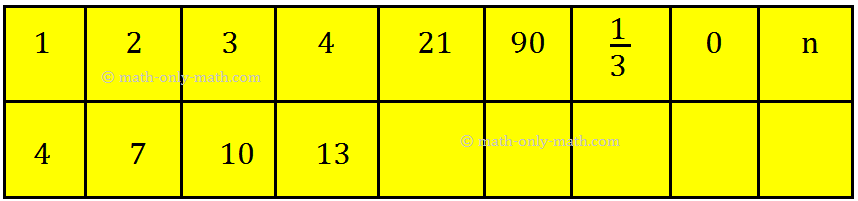
2. Look at the following pattern and fill up the missing boxes.

State the rule which connect the quantities in the different columns.

Find the general statement for n in this case.

Answer:

2. 21 → 64; 90 → 181; \(\frac{1}{3}\) → 12; 0 → 1; n → 3n + 1

General Term; n = 3n + 1

3. Complete the following table using the formula y = 2x + 2

Answer:

3. 1 → 4

3 → 8

5 → 12

15 → 32

32 → 66

4. For each sequence, find: (a) general rule (b) n^th term (c) 100^th term.

(i) 5, 10, 15, 20,..

(ii) 4, 8, 12, 16, ....

(iii) 12, 24, 36, ...

(iv) 1, 5, 9, 13,.....

Answer:

4. (i) (a) multiple of 5 (b) 5n (c) 500

(ii) (a) multiple of 4 (b) 4n (c) 4500

(iii) (a) multiple of 12 (b) 12n (c) 1200

(iv) (a) add 4 (b) 4n - 3 (c) 397

5. Find out a pattern for the relationship between the number of odd numbers and sum can be known.

Answer:

5. The pattern of the sum of fast n odd number will be n².

6. Write down the terms of the following algebraic expressions:

(i) x + y

(ii) 2a + 3b - c

(iii) 5abc² - 2ab + 7a²c

(iv) 2ab + 4ac² - 6z

Answer:

6. (i) x, y

(ii) 2a, 3b, - c

(iii) 5abc², - 2ab, 7a²c

(iv) 2ab, 4ac², - 6z

7. Which of the following groups have like terms and which have unlike terms?

(i) 3a, 8a, - 6a

(ii) 6b, - 4x, 9m

(iii) 5n, - 6p, 6y

(iv) - 16x, - 8y, - 3a

(v) - 9z, 15z, 8z

(vi) - 4r, 6r, - 9r

Answer:

7. (i) like terms

(ii) unlike terms

(iii) unlike terms

(iv) unlike terms

(v) like terms

(vi) like terms

8. Separate monomials, binomials and trinomials from the following:

3x, -xyz, m + n, ab + 2c, x + y + z, 2t + 3q + x

Answer:

8. 3x is monomial,

- xyz is monomial,

m + n is binomial

ab + 2c is binomial

x + y + z is trinomial

2t + 3q + x is trinomial

9. Write the following in exponential form

(i) a × a × b × b

(ii) a × a × a × a × a

(iii) t × t × t × t

(iv) pq × pq × pq

(v) mn × mn × mn × mn × mn

Answer:

9. (i) a²b²

(ii) a⁵

(iii) t⁴

(iv) p³q³

(v) m⁵n⁵

10. Write the following in expanded form:

(i) a³

(ii) y⁷

(iii) (pq)⁴

(iv) (ab)⁴

(v) m⁸

Answer:

10. (i) a × a × a

(ii) y × y × y × y × y × y × y

(iii) pq × pq × pq × pq 

(iv) ab × ab × ab × ab 

(v) m × m × m × m × m × m × m × m

11. Rearrange terms of the following expressions in ascending order of powers of x:

(i) x⁷, x⁴, x¹³, x¹¹, x²

(ii) 5x², 2x, 4x⁴, 3x³, 7x⁵

Answer:

11. (i)  x², x⁴, x⁷, x¹¹, x¹³

(ii) 2x, 5x², 3x³, 4x⁴,  7x⁵

12. Convert the following into algebraic expressions:

(i) The sum of x and 8

(ii) x is added to y.

(iii) The difference between x and 9, when x > 9

(iv) The difference between x and y, when x < y

(v) b is multiplied by 13

(vi) Product of a and b

(vii) p is divided by 10.

(viii) 11 divided by a.

(ix) 6 times a is added to 3 times b.

(x) 18 is subtracted from y.

(xi) 5 times x is taken away from 10.

Answer:

12. (i) x + 8

(ii) x + y.

(iii) x - 9

(iv) y - x

(v) 13b

(vi) ab

(vii) \(\frac{p}{10}\)

(viii) \(\frac{11}{a}\)

(ix) 6a + 3b.

(x) y - 18

(xi) 10 - 5x

13. Solve:

(i) x + 5 = 12

(ii) y - 2 = 10

(iii) 7p = 210

(iv) 5q = 50

(iv) x + 8 = 11

(vi) 2x - 10 = - 12

(vii) 9x = 36

(viii) 12x = - 108

Answer:

13. (i) x = 7

(ii) y = 12

(iii) p = 30

(iv) q = 10

(iv) x = 3

(vi) x = - 1

(vii) x = 4

(viii) x = -9

14. Solve and verify the result:

(i) x + 8 = 12

(ii) 15 - x = 3

(iii) 4y = - 12

(iv) x - 8 = 16

Answer:

14. (i) x = 4

(ii) x = 12

(iii) y = - 3

(iv) x = 24

15. Solve and verify:

(i) 19x - 13 = 11x + 35

(ii) 2(x - 2) - 3(x - 3) = 5(x - 5)

Answer:

15. (i) x = 6

(ii) x = 5

16. State True or False:

(i) The value of x which satisfies the equation 3x - 5 = \(\frac{5}{2}\)x - 1 is 8.

(ii) If a number n is multiplied by 3 and then 5 is subtracted from the result, I get 76. The equation to find the number is 5 - 3n = 76

(iii) A term of the expression having no literal factor is called a constant term.

(iv) The coefficient of -y in - 2x²y is (- 2x)²

(v) Richard spends $ p and earns $ q everyday. If he spends less than what he earns, then in a week he saves $ 7(p - q).

Answer:

16. (i) True

(ii) False

(iii) True

(iv) False

(v) False

17. Fill in the blanks:

(i) The coefficient of b in - ba²c is __________.

(ii) 3 times k subtracted from 9 times t is __________.

(iii) The solution of 3x + 4 = 8 - x is x = __________.

(iv) The parts of an algebraic expression which are connected by '+' or '-' sign are called its __________.

(v) There are 37 girls in a class. If x more girls join the class, then the total number of girls in the class will be __________.

Answer:

17. (i)  -a²c

(ii) 9 - 3k 

(iii) 1

(iv) terms

(v) 37 + x

18. Match the Columns

Answer:

18. (a) → (ii)

(b) → (iii)

(c) → (iv)

(d) → (i)

19. Write the following using numbers, literal numbers or variables and the fundamental operations:

(i) Area of a square = (Side x Side) sq. unit

(ii) Diameter = 2 × Radius

(iii) Circumference of circle = 2 × π × Radius

Answer:

19. (i) A = s² sq. unit; Where A = area of a square and s = side of the square

(ii) D = 2 × r; Where D = Diameter and r= Radius

(iii) C = 2πr; Where C = Circumference and r = Radius of the circle

20. Convert the following into algebraic expressions:

(i) Product of k and z

(ii) When p is added 6 times.

(iii) The sum of twice x, thrice y and z

(iv) The difference between the sum of (a and b) and c.

Answer:

20. (i) kz

(ii) 6p

(iii) 2x + 3y + z

(iv) (a + b) - c

21. Express the following in the form of equation:

(i) If 20 is subtracted from 3x, the difference is equal to the sum of x and 4.

(ii) David's age plus 15 is equal to 46.

(iii) One-fourth of a number plus 24 is equal to 72.

(iv) Six times a number plus 12 is equal to 36.

Answer:

21. (i) 3x - 20 = x + 4

(ii) x + 15 = 46

(iii) \(\frac{1}{4}\)x + 24 = 72

(iv)  6x + 122 = 36

22. Write an equation for each of the following statements:

(i) A number divided by 4 is 8.

(ii) Sum of two numbers is 28

(iii) Half of the sum of two numbers is 8.

(iv) A number multiplied by itself is 12 more than the number.

Answer:

22. (i) \(\frac{x}{4}\) = 8

(ii) x + y = 28

(iii) \(\frac{1}{2}\)(x + y) = 8.

(iv) x² = 12 + x

23. Write an equation for each of the following statements:

(i) The sum of three times x and 8 is 17.

(ii) The difference between one-fifth of x and one-tenth of x is 3.

Answer:

23. (i) 3x + 8 = 17

(ii) \(\frac{x}{5}\) - \(\frac{x}{10}\) = 3.

24. Jessica travelled 9m km on foot, 12n km by cycle and 25 km by bus. Express the total distance covered by Jessica by an algebraic expression.

Answer:

24. (9m + 12n + 25) km

25. A rectangular box has height h cm. Its length is 5 times the height and breadth is 10 cm less than the length. Express the length and breadth of the box in terms of the height.

Answer:

25. Length = 5 cm, Breadth = (5h - 10) cm

26. The length of a rectangular hall is 4 metres less than 3 times the breadth of the hall. What is the length, if the breadth is b metres?

Answer:

26. (3b - 4) metres

27. The cost of a chair is x and the cost of a cupboard is $210. If the total cost of two chairs and a cupboard is $630, find the cost of a chair.

Answer:

27. $210

28. The length of a rectangle is twice its breadth. If the perimeter is 36 metres, find the length of the rectangle.

Answer:

28. 12 metres

29. If the sum of three consecutive even numbers is 60, find the smallest of them.

Answer:

29. 18

30. Jennifer paid 36 for 3 copies and 2 pens. A pen costs 3 times as much as a copy. How much did she pay for a pen?

Answer:

30. $12

31. Sarah is thrice as old as Nancy's age. If Nancy's age is x years, what is Sarah's age?

Answer:

31. 3x

32. The difference of two numbers is 12. If you write 'p' for smaller number, how do you write the larger number?

Answer:

32. 6 + p

Algebra Page

6th Grade Page

From Solution of an Equation to HOME PAGE