Reflection of a Point in the Origin
We will discuss here how to find the reflection of a point in the origin.
Let M (a, b) be any point in the coordinate plane and O be the origin. Now join M and O, and produce it to the point M’ such that M’O = OM. Then the point M’ is the reflection of the point M in the origin. Thus, M’ is the image of M in the origin O. From the figure, we find that the coordinates of the point M’ are (-a, -b).
Thus, the reflection of the point M (a, b) in the origin is the point M’ (-a, -b)
Or
The image of the point (a, b) in the origin is the point (-a, -b).
Symbolically M \(_{o}\) (a, b) = (-a, -b).
Rules to find the
reflection of a point in the origin:
(i) Change the sign of x-coordinate i.e. abscissa.
(ii) Change the sign of y-coordinate i.e. ordinate.
For example:
(i) Reflection of the point (5, 6) in the origin is the point (-5, -6) i.e. M \(_{o}\) (5, 6) = (-5, -6)
(ii) Reflection of the point (7, -3) in the origin is the point (-7, 3) i.e. M \(_{o}\) (7, -3) = (-7, 3)
Solved examples to find the reflection of a point in the origin:
Find the points onto which the following points are mapped on reflection in the origin.
(i) (4, 9)
(ii) (-1/4, 1/6)
(iii) (10, -15)
(iv) (-a, -b)
Solution:
We know that a point (x, y) is mapped onto the point (-x, -y) on reflection in the origin.
(i) (4, 9) maps onto (-4, -9)
(ii) (-1/4, 1/6) maps onto (1/4, -1/6)
(iii) (10, -15) maps onto (-10, 15)
(iv) (-x, -y) maps onto (x, y)
● Reflection
- Position of a Point in a Plane
- Reflection of a Point in a Line
- Reflection of a Point in the x-axis
- Reflection of a Point in the y-axis
- Reflection of a Point in the Origin
- Reflection of a Point in a Line Parallel to the x-axis
- Reflection of a Point in a Line Parallel to the y-axis
- Problems on Reflection in the x-axis or y-axis
- Invariant Points for Reflection in a Line
- Reflection in Lines Parallel to Axes
- Worksheet on Reflection in the Origin
10th Grade Math
From Reflection of a Point in the Origin to HOME PAGE
Didn't find what you were looking for? Or want to know more information about Math Only Math. Use this Google Search to find what you need.
Recent Articles
-
Pictograph to Represent The Collected Data | Forming Pictograph | Math
May 07, 24 05:36 PM
Pictures or symbols are made in a pictograph to represent the collected data. So, we can say that a pictograph represents the data and gives information quickly and clearly. -
Examples of Pictographs |Pictorial Representation|Pictograph Questions
May 07, 24 05:27 PM
Some sample examples of pictographs or pictorial representation are shown, how the objects are used to give information regarding mathematical data. Read the pictograph and gather the information -
Mental Math on Time | 4th Grade Time Worksheet | Tricks | Techniques
May 07, 24 01:36 PM
In mental math on time, we will solve different types of problems on reading time to the nearest minutes, reading time to the exact minutes, use of a.m. and p.m., 24-hours clock, days in a year and ca… -
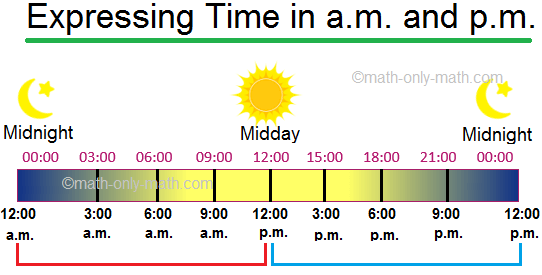
Telling Time in a.m. and p.m. | Antemeridian and Postmeridian|Examples
May 06, 24 05:54 PM
The clock shows time in 12 hour cycle. The first cycle of the hour hand completes at 12 o’clock midday or noon. The second cycle of the hour hand completes at 12 o’clock midnight. ‘a.m.’ and ‘p.m.’ ar… -
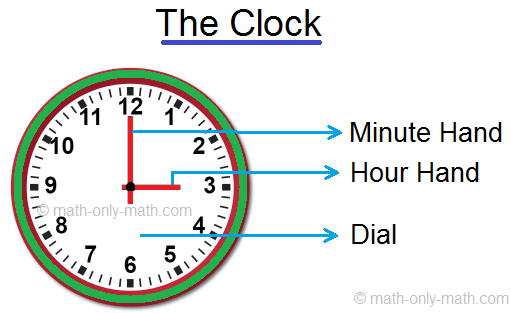
Different Ways of Reading Time | Many Ways to Read Time | Telling Time
May 06, 24 05:23 PM
What are the different ways of reading time? There are many ways to read time: (a) When hour-hand is exactly at any number and minute-hand is at 12, we read the time in full hours. If hour hand is at



New! Comments
Have your say about what you just read! Leave me a comment in the box below. Ask a Question or Answer a Question.