Plane Figures

In geometry now we will learn about the definition of plane figures. But before that let us recall, we know that solid shapes have surfaces.

Some solid shapes have plane surfaces, some curved surfaces and some are both types of surfaces.

A plane surface forms the plane figure of limited surfaces. We know about the following plane figures:

(i) Rectangle

(ii) Square

(iii) Triangle

(iv) Circle

These are all closed plane figures closed by line-segments. Now, we have to know more about such closed figures.

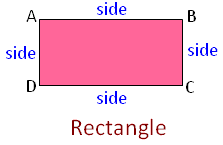
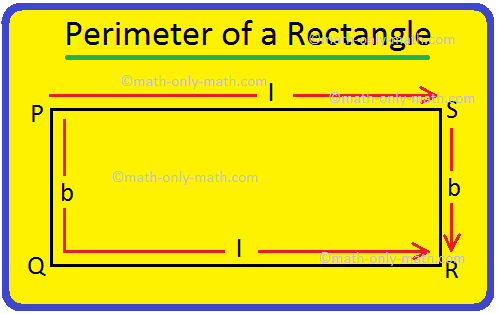
1. Rectangle: A rectangle is a plane closed figure enclosed by four line segments.

These four line segments are called the sides of the rectangle. In the above rectangle ABCD the sides are AB, DC, AD and BC.

The opposite sides of a rectangle are equal. Here the four vertices of the rectangle ABCD are A, B, C and D.

Thus, there are four sides of a rectangle. The opposite sides are equal to each other. A rectangle has four vertices.

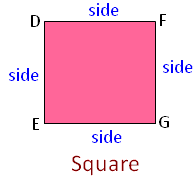
2. Square: A square is plane closed figure enclosed by four equal line-segments.

It is also a rectangle having all four sides equal. Like rectangle, the line-segments of the square are also known as sides. In the above square DEFG, there are four sides DE, EF, FG and GD; these sides are equal and they are four vertices D, E, F and G.

Thus, the closed figure of square has four equal sides and four vertices. A square is a rectangle having four equal sides.

But rectangle is not a square as only its opposite sides are equal.

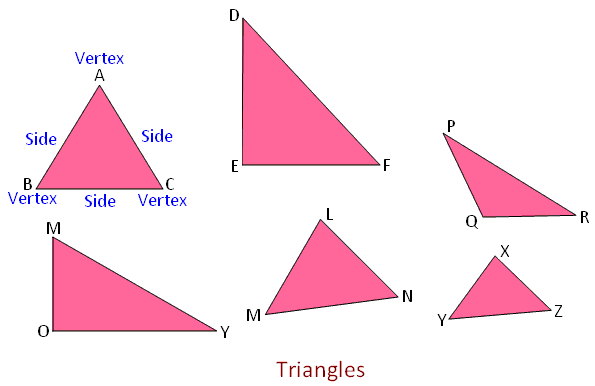
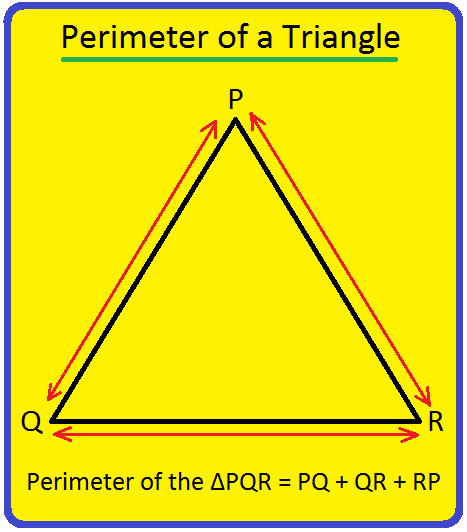
3. Triangle: A triangle is a plane closed figure enclosed by three line-segments.

The line-segments become the sides of the triangle and enclose it.

There are triangles having three sides of different lengths. Every triangle has three vertices. In the above, triangle ABC, DEF and PQR are of different shapes.

Thus, a triangle has three sides and three vertices.

4. Circle: There is a plane closed figure shown here. It is different from that of the figures shown earlier. It is called a circle.

A circle is a plane closed figure enclosed by a curve, having no sides and no corner (vertex). Every point in the curve is situated at equal distance from a definite point within the closed figure.

The closed figure shown to the above is a circle. It has a point O within it from which the closing curve is equidistant to every point on the circle.

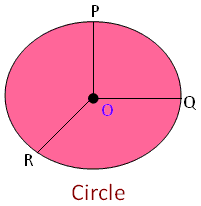
Centre: It is point within the circle which is equidistant from every point of the curve which encloses the circle ⊙.  

In the given circle, O is the centre of the circle. A circle is called by its centre’s name i.e., as circle ⊙.

Radius: The distance between the centre and any point situated at the curve closing the circle is called the radius.

In the above figure OP, OQ and OR are radii. Every radius of a circle has the same length, i.e., all the radii of a circle are equal.

Thus, OP = OQ = OR. The radius is denoted by ‘r’.

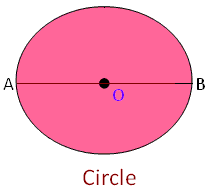
Diameter: The line-segment passing through the centre and joining the two points situated at the curve closing the circle is called the diameter.

Here, AOB or AB is the diameter of the circle O.

AOB = AO + OB, i.e., diameter = radius + radius

Thus, diameter = 2 × radius.

Circumference: The curve closing the circle is known as circumference. Every point on the circumference is equidistant from the centre.

⊙ The plane surfaces (like rectangle, triangle, circle, etc.) are called two dimensional (2-D) figures as they have length and breadth.

The plane figures in third grade geometry will help the kids to understand all the closed plane shapes closed by line-segments.

3rd Grade Math Lessons

From Plane Figures to HOME PAGE