Subscribe to our ▶️YouTube channel🔴 for the latest videos, updates, and tips.
Home | About Us | Contact Us | Privacy | Math Blog
Focal Distance of a Point on the Hyperbola
What is the focal distance of a point on the hyperbola?
The sum of the focal distance of any point on a hyperbola is constant and equal to the length of the transverse axis of the hyperbola.
Let P (x, y) be any point on the hyperbola x2a2 - y2b2 = 1.a
Let MPM' be the perpendicular through P on directrices ZK and Z'K'. Now by definition we get,
SP = e ∙ PM
⇒ SP = e ∙ NK
⇒ SP = e (CN - CK)
⇒ SP = e(x - ae)
⇒ SP = ex - a ………………..…….. (i)
and
S'P = e ∙ PM'
⇒ S'P = e ∙ (NK')
⇒ S'P = e (CK' + CN)
⇒ S'P = e (ae + x)
⇒ S'P = a + ex ………………..…….. (ii)
Therefore, S'P - SP = (a + ex) - (ex - a) = a + ex - ex + a = 2a = transverse axis.
Hence, the sum of the focal distance of a point P (x, y) on the hyperbola x2a2 - y2b2 = 1 is constant and equal to the length of the transverse axis (i.e., 2a) of the hyperbola.
Note: This property leads to an alternative definition of hyperbola as follows:
If a point moves on a plane in such a way that the sum of its distances from two fixed points on the plane is always a constant then the locus traced out by the moving point on the plane is called a hyperbola and the two fixed points are the two foci of the hyperbola.
Solved example to find the focal distance of any point on a hyperbola:
Find the focal distance of a point on the hyperbola 9x2 - 16y2 - 18x + 32y - 151 = 0.
Solution:
The given equation of the hyperbola is 9x2 - 16y2 - 18x + 32y - 151 = 0.
From the above equation we get,
9x2 - 18x - 16y2 + 32y = 151
⇒ 9(x2 - 2x) - 16(y2 - 2y) = 151
⇒ 9(x2 - 2x + 1) - 16(y2 - 2y + 1) = 151 + 9 - 16
⇒ 9(x - 1)2 - 16(y - 1)2 = 144
⇒ (x−1)216 - (y−1)29 = 1 ………………….. (i)
Now transfering the origin at (1, 1) without rotating the coordinate axes and denoting the new coordinates with respect to the new axes by x and y, we have
x = X + 1 and y = Y + 1 ………………….. (ii)
Using these relations, equation (i) reduces to
X242 - Y232 = 1 ……………………… (iii)
This is the form of X2a2 - Y2b2 = 1 (a2 > b2 ) where a = 4 and b = 3
Now, we get that a > b.
Hence, the equationX242 - Y232 = 1 represents an hyperbola
whose transverse axes along X and conjugate axes along Y axes.
Therefore, the focal distance of a point on the hyperbola 9x2 - 16y2 - 18x + 32y - 151 = 0 is transverse axis = 2a = 2 ∙ 4 = 8 units.
From Focal Distance of a Point on the Hyperbola to HOME PAGE
Didn't find what you were looking for? Or want to know more information about Math Only Math. Use this Google Search to find what you need.
Recent Articles
-
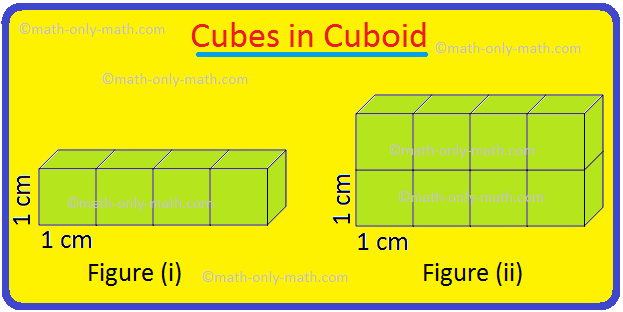
Volume of a Cuboid | Volume of Cuboid Formula | How to Find the Volume
Jul 20, 25 12:58 PM
Cuboid is a solid box whose every surface is a rectangle of same area or different areas. A cuboid will have a length, breadth and height. Hence we can conclude that volume is 3 dimensional. To measur… -
5th Grade Volume | Units of Volume | Measurement of Volume|Cubic Units
Jul 20, 25 10:22 AM
Volume is the amount of space enclosed by an object or shape, how much 3-dimensional space (length, height, and width) it occupies. A flat shape like triangle, square and rectangle occupies surface on… -
Worksheet on Area of a Square and Rectangle | Area of Squares & Rectan
Jul 19, 25 05:00 AM
We will practice the questions given in the worksheet on area of a square and rectangle. We know the amount of surface that a plane figure covers is called its area. 1. Find the area of the square len… -
Area of Rectangle Square and Triangle | Formulas| Area of Plane Shapes
Jul 18, 25 10:38 AM
Area of a closed plane figure is the amount of surface enclosed within its boundary. Look at the given figures. The shaded region of each figure denotes its area. The standard unit, generally used for… -
What is Area in Maths? | Units to find Area | Conversion Table of Area
Jul 17, 25 01:06 AM
The amount of surface that a plane figure covers is called its area. It’s unit is square centimeters or square meters etc. A rectangle, a square, a triangle and a circle are all examples of closed pla…


New! Comments
Have your say about what you just read! Leave me a comment in the box below. Ask a Question or Answer a Question.