Factorize the Difference of Two Squares
Explain how to factorize the difference of two squares?
We know the formula (a2 – b2) = (a + b)(a - b) is used to factorize the algebraic expressions.Solved problems to factorize the difference of two squares:
1. Factorize:
(i) y2 - 121Solution:
We can write y2 – 121 as a2 - b2.
= (y)2 - (11)2, we know 121 = 11 times 11 = 112.
Now we will apply the formula of a2 - b2 = (a + b) (a – b)
= (y + 11)(y - 11).
(ii) 49x2 - 16y2
Solution:
We can write 49x2 - 16y2 as a2 - b2 = (a + b) (a – b)
= (7x)2 - (4y)2,
[Since we know 49x2 = 7x times 7x which is (7x)2 and (4y)2 = 4y times 4y which is (4y)2].
= (7x + 4y) (7x - 4y).
2. Factor the following:
(i) 48a2 - 243b2Solution:
We can write 48a2 - 243b2 as a2 - b2
= 3(16a2 - 81b2), taking common ‘3’ from both the terms. = 3 ∙ {(4a)2 - (9b)2}
Now we will apply the formula of a2 - b2 = (a + b) (a – b)
= 3(4a + 9b) (4a - 9b).
(ii) 3x3 - 48x
Solution:
3x3 - 48x
= 3x(x2 - 16), taking common ‘3x’ from both the terms.
We can write x2 - 16 as a2 - b2
= 3x(x2 - 42)
Now we will apply the formula of a2 - b2 = (a + b)(a – b)
= 3x(x + 4)(x - 4).
3. Factor the expressions:
(i) 25(x + 3y)2 - 16 (x - 3y)2Solution:
We can write 25(x + 3y)2 - 16 (x - 3y)2 as a2 - b2.
= [5(x + 3y)]2 - [4(x - 3y)]2
Now using the formula of a2 – b2 = (a + b)(a – b) we get,
= [5(x + 3y) + 4(x - 3y)] [5(x + 3y) - 4(x - 3y)]
= [5x + 15y + 4x - 12y] [5x + 15y - 4x + 12y], using distributive property
= [9x + 3y] [x + 27y], simplifying
= 3[3x + y] [x + 27y]
Solution:
We can write 4a2 - 16/(25a2) as a2 – b2.
(2a)2 - (4/5a)2, since 4a2 = (2a)2, 16 = 42 and 25a2 = (5a)2
Now we will express as a2 – b2 = (a + b) (a – b)
(2a + 4/5a)(2a - 4/5a)
8th Grade Math Practice
From Factorize the Difference of Two Squares to HOME PAGE
Didn't find what you were looking for? Or want to know more information about Math Only Math. Use this Google Search to find what you need.
Recent Articles
-
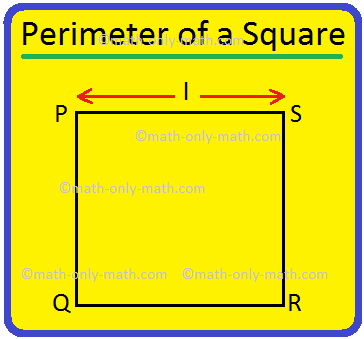
Perimeter of a Square | How to Find the Perimeter of Square? |Examples
Apr 25, 24 05:34 PM
We will discuss here how to find the perimeter of a square. Perimeter of a square is the total length (distance) of the boundary of a square. We know that all the sides of a square are equal. Perimete… -
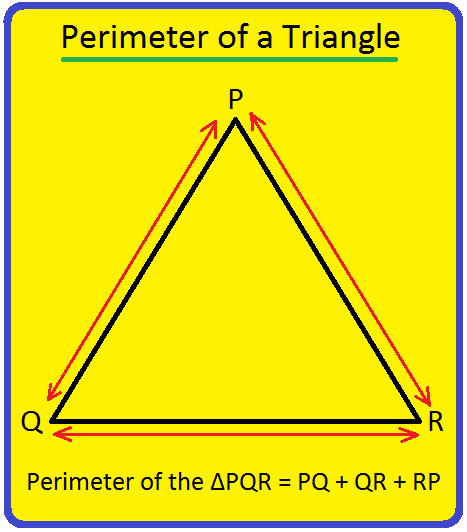
Perimeter of a Triangle | Perimeter of a Triangle Formula | Examples
Apr 25, 24 05:13 PM
We will discuss here how to find the perimeter of a triangle. We know perimeter of a triangle is the total length (distance) of the boundary of a triangle. Perimeter of a triangle is the sum of length… -
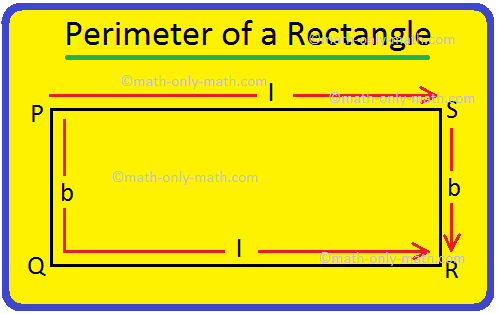
Perimeter of a Rectangle | How to Find the Perimeter of a Rectangle?
Apr 25, 24 03:45 PM
We will discuss here how to find the perimeter of a rectangle. We know perimeter of a rectangle is the total length (distance) of the boundary of a rectangle. ABCD is a rectangle. We know that the opp… -
Dividing 3-Digit by 1-Digit Number | Long Division |Worksheet Answer
Apr 24, 24 03:46 PM
Dividing 3-Digit by 1-Digit Numbers are discussed here step-by-step. How to divide 3-digit numbers by single-digit numbers? Let us follow the examples to learn to divide 3-digit number by one-digit nu… -
Symmetrical Shapes | One, Two, Three, Four & Many-line Symmetry
Apr 24, 24 03:45 PM
Symmetrical shapes are discussed here in this topic. Any object or shape which can be cut in two equal halves in such a way that both the parts are exactly the same is called symmetrical. The line whi…