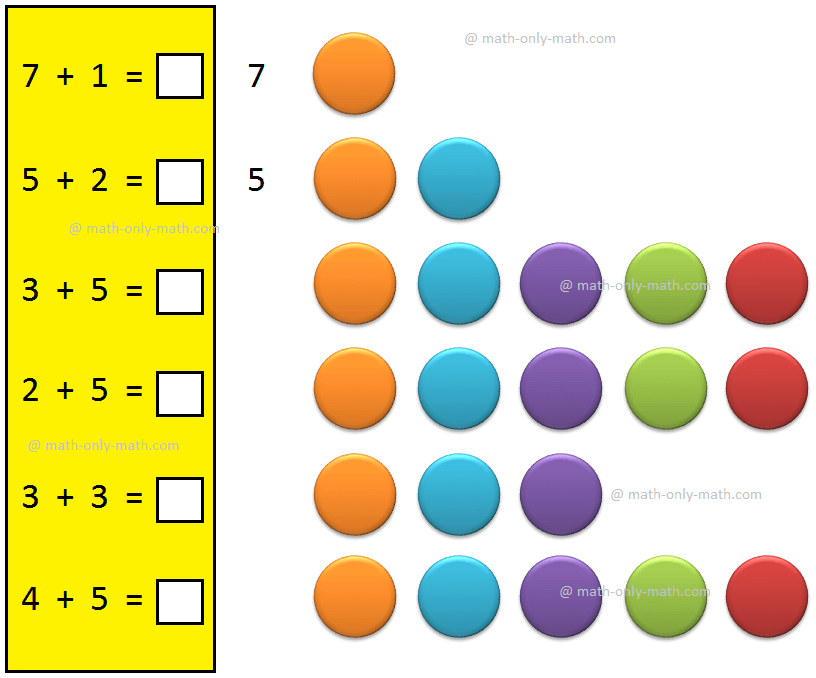Cube of the Difference of Two Binomials
What is the formula for the cube of the difference of two binomials?
To determine cube of a number means multiplying a number with itself three times similarly, cube of a binomial means multiplying a binomial with itself three times.
(a - b) (a - b) (a - b) = (a - b)3
or, (a - b) (a - b) (a - b) = (a - b) (a - b)2
= (a – b) (a2 + b2 - 2ab),
[Using the formula of (a + b) 2 = a2 - 2ab + b2]
= a (a2 + b2 – 2ab) – b (a2 + b2 – 2ab)
= a3 + ab2 – 2a2b – ba2 – b3 + 2ab2
= a3 – 3a2b + 3ab2 – b3
Therefore, (a - b)3 = a3 – 3a2b + 3ab2 – b3
Thus, we can write it as; a = first term, b = second term
(First term – Second term)3 = (first term)3 - 3 (first term)2 (second term) + 3 (first term) (second term)2 - (second term)3
So, the formula for the cube of the difference of two terms is written as:
(a - b)3 = a3 – 3a2b + 3ab2 – b3
= a3 – b3 – 3ab (a - b)
Worked-out examples to find the cube of the difference of two binomials:
1. Determine the expansion of (3x – 4y)3Solution:
We know, (a - b)3 = a3 – 3a2b + 3ab2 – b3
(3x – 4y)3
Here, a = 3x, b = 4y
= (3x)3 – 3 (3x)2 (4y) + 3 (3x) (4y)2 – (4y)3
= 27x3 – 3 (9x2) (4y) + 3 (3x) (16y2) – 64y3
= 27x3 – 108x2y + 144xy2 – 64y3
Therefore, (3x – 4y)3 = 27x3 – 108x2y + 144xy2 – 64y3
2. Use the formula and evaluate (997)3
Solution:
(997)3 = (1000 – 3)3
We know, (a - b)3 = a3 – 3a2b + 3ab2 – b3
Here, a = 1000, b = 3
(1000 – 3)3
= (1000)3 – 3 (1000)2 (3) + 3 (1000) (3)2 – (3)3
= 1000000000 – 9 (1000000) + (3000) 9 – 27
= 1000000000 – 9000000 + 27000 – 27
= 991026973
Therefore, (997)3 = 991026973
Thus, to expand the cube of the difference of two binomials we can use the formula to evaluate.
7th Grade Math Problems
8th Grade Math Practice
From Cube of The Difference of Two Binomials to HOME PAGE
Didn't find what you were looking for? Or want to know more information about Math Only Math. Use this Google Search to find what you need.
Recent Articles
-
Adding 1-Digit Number | Understand the Concept one Digit Number
Apr 26, 24 01:55 PM
Understand the concept of adding 1-digit number with the help of objects as well as numbers. -
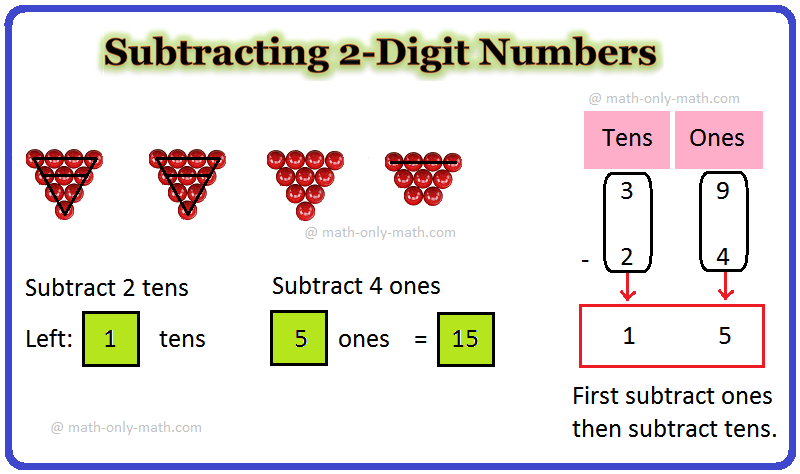
Subtracting 2-Digit Numbers | How to Subtract Two Digit Numbers?
Apr 26, 24 12:36 PM
In subtracting 2-digit numbers we will subtract or minus a two-digit number from another two-digit number. To find the difference between the two numbers we need to ‘ones from ones’ and ‘tens from -
1st Grade Word Problems on Subtraction | Subtracting 2-Digit Numbers
Apr 26, 24 12:06 PM
In 1st grade word problems on subtraction students can practice the questions on word problems based on subtraction. This exercise sheet on subtraction can be practiced by the students to get more ide… -
Subtracting 1-Digit Number | Subtract or Minus Two One-Digit Number
Apr 26, 24 11:21 AM
In subtracting 1-digit number we will subtract or minus one-digit number from one-digit number or one-digit number from 2-digit number and find the difference between them. We know that subtraction me… -
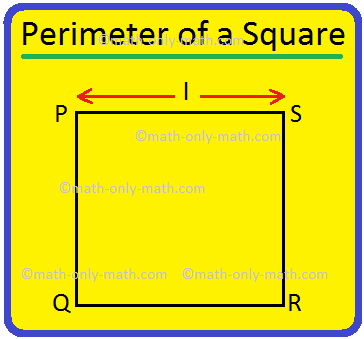
Perimeter of a Square | How to Find the Perimeter of Square? |Examples
Apr 25, 24 05:34 PM
We will discuss here how to find the perimeter of a square. Perimeter of a square is the total length (distance) of the boundary of a square. We know that all the sides of a square are equal. Perimete…