Equally Inclined Lines
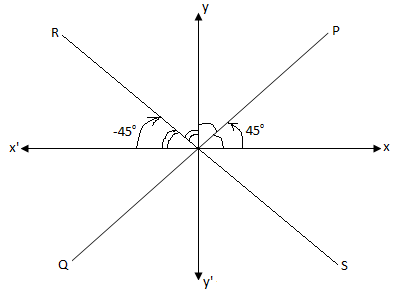
By the meaning of equally inclined lines, we mean that the lines which make equal angles with both the co-ordinate axes.
The above diagram shows that PQ and RS are the two equally inclined lines.
From the above diagram it is clear that;
For PQ: Inclination θ = 45°,
Therefore, slope = tan 45° = 1.
For RS: Inclination θ = -45°,
Therefore, slope = tan (-45°) = -1.
Solved example on equally inclined lines:
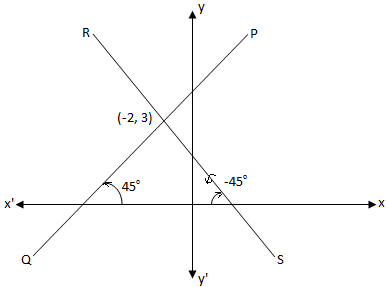
Find the equation of the lines which is passes through the point (-2. 3) and equally inclined to the co-ordinate axes.
Solution:
From the above diagram it is clear that; there are two lines PQ and RS, equally inclined to the co-ordinate axes.
For line PQ: m = tan 45° = 1
and (x\(_{1}\), y\(_{1}\)) = (-2, 3)
Therefore, its equation: y – y\(_{1}\) = m(x – x\(_{1}\))
⟹ y – 3 = 1(x + 2)
⟹ y - 3 = x + 2
⟹ y = x + 5
For line RS: m = tan (-45°) = -1
and (x\(_{1}\), y\(_{1}\)) = (-2, 3)
Therefore, its equation: y – y\(_{1}\) = m(x – x\(_{1}\))
⟹ y – 3 = -1(x + 2)
⟹ y - 3 = -x - 2
⟹ y = -x + 1
Therefore, the required equations are y = x + 5 and y = -x + 1
From Equally Inclined Lines to HOME
Didn't find what you were looking for? Or want to know more information about Math Only Math. Use this Google Search to find what you need.
Recent Articles
-
Perimeter of a Square | How to Find the Perimeter of Square? |Examples
Apr 25, 24 05:34 PM
We will discuss here how to find the perimeter of a square. Perimeter of a square is the total length (distance) of the boundary of a square. We know that all the sides of a square are equal. Perimete… -
Perimeter of a Triangle | Perimeter of a Triangle Formula | Examples
Apr 25, 24 05:13 PM
We will discuss here how to find the perimeter of a triangle. We know perimeter of a triangle is the total length (distance) of the boundary of a triangle. Perimeter of a triangle is the sum of length… -
Perimeter of a Rectangle | How to Find the Perimeter of a Rectangle?
Apr 25, 24 03:45 PM
We will discuss here how to find the perimeter of a rectangle. We know perimeter of a rectangle is the total length (distance) of the boundary of a rectangle. ABCD is a rectangle. We know that the opp… -
Dividing 3-Digit by 1-Digit Number | Long Division |Worksheet Answer
Apr 24, 24 03:46 PM
Dividing 3-Digit by 1-Digit Numbers are discussed here step-by-step. How to divide 3-digit numbers by single-digit numbers? Let us follow the examples to learn to divide 3-digit number by one-digit nu… -
Symmetrical Shapes | One, Two, Three, Four & Many-line Symmetry
Apr 24, 24 03:45 PM
Symmetrical shapes are discussed here in this topic. Any object or shape which can be cut in two equal halves in such a way that both the parts are exactly the same is called symmetrical. The line whi…