Word Problems using Proportion
We will learn how to solve word problems
using proportion. If four numbers p, q, r and s are in proportion, then p and s are called the extreme terms and q and r are called the middle terms. Then, the product of extreme terms (i.e. p × s) is equal to the product of middle terms (i.e. r × s).
Therefore, p : q : : r : s ⇒ ps = qr
Solved problems using proportion:
1. Determine if the following are in proportion. If yes write them in proper form.
(i) 32, 48, 140, 210; (ii) 6, 9, 10 and 16
Solution:
(i) 32, 48, 140, 210
32 : 48 = 32/48 = 2/3 = 2 : 3
140 : 210 = 140/210 = 2/3 = 2 : 3
So, 32 : 48 = 140 : 210
Therefore, 32, 48, 140, 210 are in proportion.
i.e., 32 : 48 :: 140 : 210
(ii) 6, 9, 10 and 16
6 : 9 = 6/9 = 2/3 = 2 : 3
10 : 16 = 10/16 = 5/8 = 5 : 8
Since, 6 : 9 ≠ 10 : 16 therefore, 6, 9, 10 and 16 are not in proportion.
2. The numbers 8, x, 9 and 36 are in proportion. Find x.
Solution:
The numbers 8, x, 9 and 36 are in proportion
⇒ 8 : x = 9 : 36
⇒ x × 9 = 8 × 36, [Since, the product of the means = the product of the extremes]
⇒ x = (8 × 36)/9
⇒ x = 32
3. If x : 15 = 8 : 12; find the value of x.
Solution:
⇒ x × 12 = 15 × 8, [Since, the product of the extremes = the product of the means]
⇒ x = (15 × 8)/12
⇒ x = 10
4. If 4, x, 32 and 40 are in proportion, find the value of x.
Solution:
4, x, 32 and 40 are in proportion, i.e., 4 : x :: 32 : 40
Now, product of extremes = 4 × 40 = 160
And product of means = x × 32
We know that in a proportion product of extremes = product of means
i.e., 160 = x × 32
If we multiply 32 by 5, we get 160
i.e., 5 × 32 = 160
So, x = 5
Hence, 4, 5, 32 and 40 are in proportion.
More word problems using proportion:
5. If x : y = 4 : 5 and y : z = 6 : 7; find x : y : z.
Solution:
x : y = 4 : 5 = 4/5 : 1, [Dividing each term by 5]
y : z = 6 : 7 = 1 : 7/6, [Dividing each term by 6]
In both the given ratios, the quantity y is common, so we have made the value of y same i.e., 1.
Thus; x : y : z = 4/5 : 1 : 7/6
= (4/5 × 30) : (1 × 30) : (7/6 × 30), [Multiply all the terms by the L.C.M. of 5 and 6 i.e., 30]
= 24 : 30 : 35
Therefore, x : y : z = 24 : 30 : 35
6. The ratio of the length to the width of a sheet of paper is 3 : 2. If the length is 12 cm, find its width.
Solution:
Let the width of the sheet of paper be x cm
The length of the sheet of paper be 12 cm. (Given)
According to the given statement,
12 : x = 3 : 2
⇒ x × 3 = 12 × 2, [Since, the product of the means = the product of the extremes]
⇒ x = (12 × 2)/3
⇒ x = 8
Therefore, the width of the sheet of paper is 8 cm.
7. The length and breadth of a rectangle are in the ratio 5 : 4. If its length is 80 cm, find the breadth.
Solution:
Let the breadth of the rectangle be x cm
Then, 5 : 4 :: 80 : x
⇒ 5/4 = 80/x
To get 80 in the numerator, we have to multiply 5 by 16. So, we also multiply the denominator of 5/4 i.e. 4 by 16
Thus, 5/4 = 80/(4 × 16) = 80/64
So, x = 64
Hence, breadth of the rectangle = 64 cm.
From, the above word problems using proportion we get the clear concept how to find whether the two ratios form a proportion or not and word problems.
6th Grade Page
From Word Problems using Proportion to HOME PAGE
Didn't find what you were looking for? Or want to know more information about Math Only Math. Use this Google Search to find what you need.
Recent Articles
-
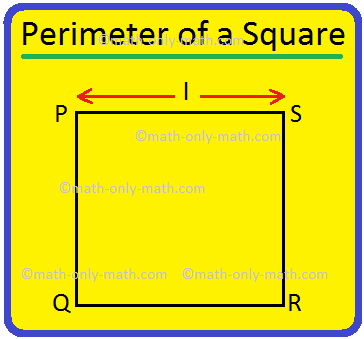
Perimeter of a Square | How to Find the Perimeter of Square? |Examples
Apr 25, 24 05:34 PM
We will discuss here how to find the perimeter of a square. Perimeter of a square is the total length (distance) of the boundary of a square. We know that all the sides of a square are equal. Perimete… -
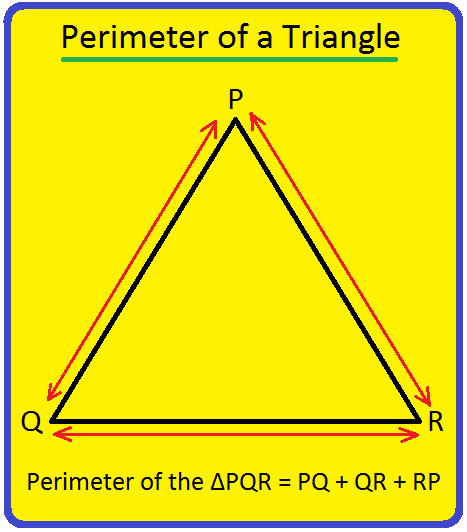
Perimeter of a Triangle | Perimeter of a Triangle Formula | Examples
Apr 25, 24 05:13 PM
We will discuss here how to find the perimeter of a triangle. We know perimeter of a triangle is the total length (distance) of the boundary of a triangle. Perimeter of a triangle is the sum of length… -
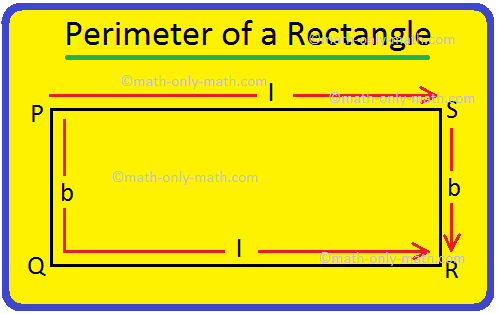
Perimeter of a Rectangle | How to Find the Perimeter of a Rectangle?
Apr 25, 24 03:45 PM
We will discuss here how to find the perimeter of a rectangle. We know perimeter of a rectangle is the total length (distance) of the boundary of a rectangle. ABCD is a rectangle. We know that the opp… -
Dividing 3-Digit by 1-Digit Number | Long Division |Worksheet Answer
Apr 24, 24 03:46 PM
Dividing 3-Digit by 1-Digit Numbers are discussed here step-by-step. How to divide 3-digit numbers by single-digit numbers? Let us follow the examples to learn to divide 3-digit number by one-digit nu… -
Symmetrical Shapes | One, Two, Three, Four & Many-line Symmetry
Apr 24, 24 03:45 PM
Symmetrical shapes are discussed here in this topic. Any object or shape which can be cut in two equal halves in such a way that both the parts are exactly the same is called symmetrical. The line whi…