Trigonometric Ratios of Angle \(\frac{A}{3}\)

We will learn about the trigonometric ratios of angle \(\frac{A}{3}\) in terms of angle A. 

How to express sin A, cos A and tan A in terms of \(\frac{A}{3}\)?

(i) For all values of the angle A we know that, sin 3A = 3 sin A - 4 sin\(^{3}\) A

Now replacing A by \(\frac{A}{3}\) in the above relation then we obtain the relation as,

sin A = 3 sin \(\frac{A}{3}\) - 4 sin\(^{3}\) \(\frac{A}{3}\)


(ii) For all values of the angle A we know that, cos 3A= 4 cos\(^{3}\) A - 3 cos A

Now replacing A by \(\frac{A}{3}\) in the above relation then we obtain the relation as,

cos A = 4 cos\(^{3}\) \(\frac{A}{3}\) - 3 cos \(\frac{A}{3}\)


(iii) For all values of the angle A we know that, tan 3A = \(\frac{3  tan  A  -  tan^{3}  A}{1  -  3  tan^{2}  A}\)

Now replacing A by \(\frac{A}{3}\) in the above relation then we obtain the relation as,

tan A = \(\frac{3  tan  \frac{A}{3}  -  tan^{3}  \frac{A}{3}}{1  -  3  tan^{2}  \frac{A}{3}}\)

















11 and 12 Grade Math

From Trigonometric Ratios of Angle A/3 to HOME PAGE




Didn't find what you were looking for? Or want to know more information about Math Only Math. Use this Google Search to find what you need.



Share this page: What’s this?

Recent Articles

RSS

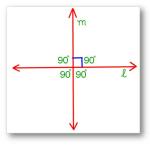
  1. Perpendicular Lines | What are Perpendicular Lines in Geometry?|Symbol

    Apr 19, 24 02:46 AM

    Perpendicular Lines
    In perpendicular lines when two intersecting lines a and b are said to be perpendicular to each other if one of the angles formed by them is a right angle. In other words, Set Square Set Square If two…

    Read More

  2. Fundamental Geometrical Concepts | Point | Line | Properties of Lines

    Apr 19, 24 01:55 AM

    Point P
    The fundamental geometrical concepts depend on three basic concepts — point, line and plane. The terms cannot be precisely defined. However, the meanings of these terms are explained through examples.

    Read More

  3. What is a Polygon? | Simple Closed Curve | Triangle | Quadrilateral

    Apr 18, 24 02:15 AM

    What is a polygon? A simple closed curve made of three or more line-segments is called a polygon. A polygon has at least three line-segments.

    Read More

  4. Simple Closed Curves | Types of Closed Curves | Collection of Curves

    Apr 18, 24 01:36 AM

    Closed Curves Examples
    In simple closed curves the shapes are closed by line-segments or by a curved line. Triangle, quadrilateral, circle, etc., are examples of closed curves.

    Read More

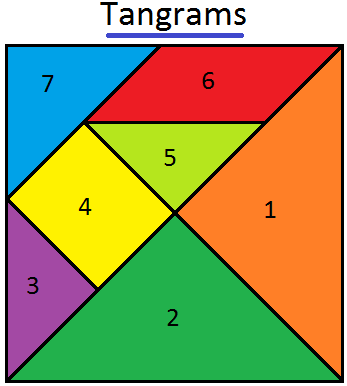
  5. Tangrams Math | Traditional Chinese Geometrical Puzzle | Triangles

    Apr 18, 24 12:31 AM

    Tangrams
    Tangram is a traditional Chinese geometrical puzzle with 7 pieces (1 parallelogram, 1 square and 5 triangles) that can be arranged to match any particular design. In the given figure, it consists of o…

    Read More