Subscribe to our ▶️YouTube channel🔴 for the latest videos, updates, and tips.
Home | About Us | Contact Us | Privacy | Math Blog
tan 3A in Terms of A
We will learn how to express the multiple angle of tan 3A in terms of A or tan 3A in terms of tan A.
Trigonometric function of tan 3A in terms of tan A is also known as one of the double angle formula.
If A is a number or angle then we have, tan 3A = 3tanA−tan3A1−3tan2A
Now we will proof the above multiple angle formula step-by-step.
Proof: tan 3A
= tan (2A + A)
= tan2A+tanA1−tan2A⋅tanA
= 2tanA1−tan2A+tanA1−2tanA1−tan2A⋅tanA
= 2tanA+tanA−tan3A1−tan2A−2tan2A
= 3tanA−tan3A1−3tan2A
Therefore, tan 3A = 3tanA−tan3A1−3tan2A
Note:
(i) In the above formula we should note that the angle on the R.H.S. of the formula is one-third of the angle on L.H.S. Therefore, tan 30° = 3tan10°−tan310°1−3tan210°.
(ii) The value of tan 3A can also be obtain by putting A = B = C in the formula
tan (A + B + C) = tanA+tanB+tanC−tanAtanBtanC1−tanAtanB−tanBtanC−tanCtanA
- sin 2A in Terms of A
- cos 2A in Terms of A
- tan 2A in Terms of A
- sin 2A in Terms of tan A
- cos 2A in Terms of tan A
- Trigonometric Functions of A in Terms of cos 2A
- sin 3A in Terms of A
- cos 3A in Terms of A
- tan 3A in Terms of A
- Multiple Angle Formulae
11 and 12 Grade Math
From tan 3A in Terms of tan A to HOME PAGE
Didn't find what you were looking for? Or want to know more information about Math Only Math. Use this Google Search to find what you need.
Recent Articles
-
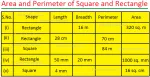
Worksheet on Area of a Square and Rectangle | Area of Squares & Rectan
Jul 19, 25 05:00 AM
We will practice the questions given in the worksheet on area of a square and rectangle. We know the amount of surface that a plane figure covers is called its area. 1. Find the area of the square len… -
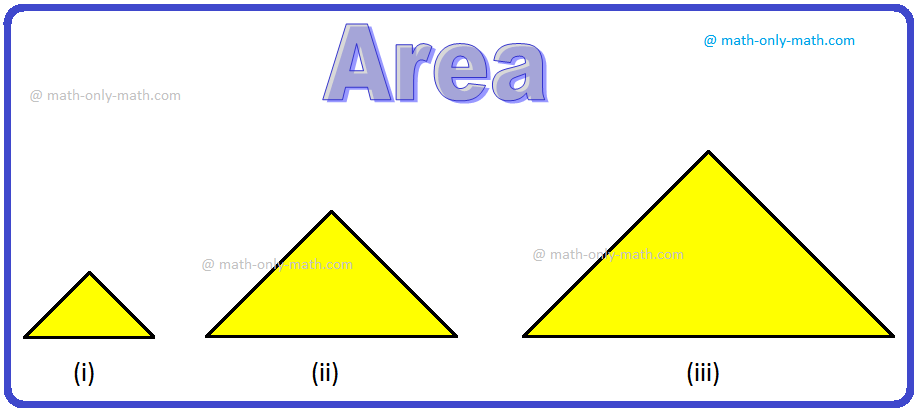
Area of Rectangle Square and Triangle | Formulas| Area of Plane Shapes
Jul 18, 25 10:38 AM
Area of a closed plane figure is the amount of surface enclosed within its boundary. Look at the given figures. The shaded region of each figure denotes its area. The standard unit, generally used for… -
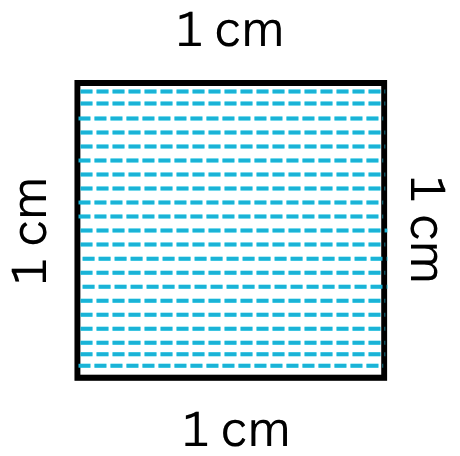
What is Area in Maths? | Units to find Area | Conversion Table of Area
Jul 17, 25 01:06 AM
The amount of surface that a plane figure covers is called its area. It’s unit is square centimeters or square meters etc. A rectangle, a square, a triangle and a circle are all examples of closed pla… -
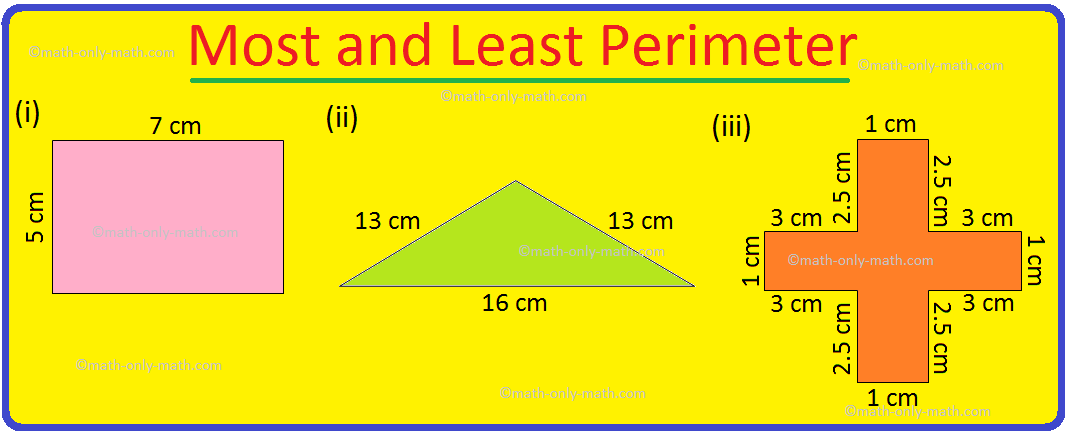
Worksheet on Perimeter | Perimeter of Squares and Rectangle | Answers
Jul 17, 25 12:40 AM
Practice the questions given in the worksheet on perimeter. The questions are based on finding the perimeter of the triangle, perimeter of the square, perimeter of rectangle and word problems. I. Find… -
Formation of Square and Rectangle | Construction of Square & Rectangle
Jul 16, 25 11:46 PM
In formation of square and rectangle we will learn how to construct square and rectangle. Construction of a Square: We follow the method given below. Step I: We draw a line segment AB of the required…

New! Comments
Have your say about what you just read! Leave me a comment in the box below. Ask a Question or Answer a Question.