Square of The Difference of Two Binomials
How to find the square of the difference of two binomials?
(a - b) (a - b) = a(a - b) - b(a - b)
= a2 - ab - ba + b2
= a2 - 2ab + b2
= a2 + b2 - 2ab
Therefore, (a - b)2 = a2 + b2 - 2ab
Square of the difference of two terms = square of 1st term + square of 2nd term - 2 × fist term × second term
This is called the binomial square.
It is stated as: the square of the difference of two binomials (two unlike terms) is the square of the first term plus the second term minus twice the product of the first and the second term.
Worked-out examples on square of the difference of two binomials:
Solution:
Square of 1st term + square of 2nd term - 2 × fist term × second term
Here, a = 4x and y = 7y
= (4x)2 + (7y)2 - 2 (4x) (7y)
= 16x2 + 49y2 - 56xy
Therefore, (4x + 7y)2 = 16x2 + 49y2 - 56xy.
2. Expand (3m - 5/6 n)2 using the formula of (a - b)2.
Solution:
We know (a - b)2 = a2 + b2 - 2ab
Here, a = 3m and b = 5/6 n
= (3m)2 + (5/6 n)2 - 2 (3m) (5/6 n)
= 9 m2 + 25/36 n2 -
= 9 m2 + 25/36 n2 - 5 mn
Therefore, (3m - 5/6 n)2 = 9 m2 + 25/36 n2 - 5 mn.
3. Evaluate (999)2 using the identity.
Solution:
(999)2 = (1000 – 1)2
We know, (a – b)2 = a2 + b2 – 2ab
Here, a = 1000 and b = 1
(1000 – 1)2
= (1000)2 + (1)2 – 2 (1000) (1)
= 1000000 + 1 – 2000
= 998001
Therefore, (999)2 = 998001
4. Use the formula of square of the difference of two terms to find the product of (0.1 m – 0.2 n) (0.1 m – 0.2 n).
Solution:
(0.1 m – 0.2 n) (0.1 m – 0.2 n) = (0.1 m – 0.2 n)2
We know (a – b)2 = a2 + b2 – 2ab
Here, a = 0.1 m and b = 0.2 n
= (0.1 m)2 + (0.2 n) 2 - 2 (0.1 m) (0.2 n)
= 0.01 m2 + 0.04 n2 - 0.04 mn
Therefore, (0.1 m – 0.2 n) (0.1 m – 0.2 n) = 0.01 m2 + 0.04 n2 - 0.04 mn
From the above solved problems we come to know square of a number means multiplying a number with itself, similarly, square of the difference of two binomial means multiplying the binomial by itself.
7th Grade Math Problems
8th Grade Math Practice
From Square of The Difference of Two Binomials to HOME PAGE
Didn't find what you were looking for? Or want to know more information about Math Only Math. Use this Google Search to find what you need.
Recent Articles
-
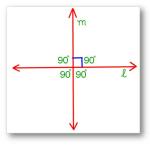
Perpendicular Lines | What are Perpendicular Lines in Geometry?|Symbol
Apr 19, 24 02:46 AM
In perpendicular lines when two intersecting lines a and b are said to be perpendicular to each other if one of the angles formed by them is a right angle. In other words, Set Square Set Square If two… -
Fundamental Geometrical Concepts | Point | Line | Properties of Lines
Apr 19, 24 01:55 AM
The fundamental geometrical concepts depend on three basic concepts — point, line and plane. The terms cannot be precisely defined. However, the meanings of these terms are explained through examples. -
What is a Polygon? | Simple Closed Curve | Triangle | Quadrilateral
Apr 18, 24 02:15 AM
What is a polygon? A simple closed curve made of three or more line-segments is called a polygon. A polygon has at least three line-segments. -
Simple Closed Curves | Types of Closed Curves | Collection of Curves
Apr 18, 24 01:36 AM
In simple closed curves the shapes are closed by line-segments or by a curved line. Triangle, quadrilateral, circle, etc., are examples of closed curves. -
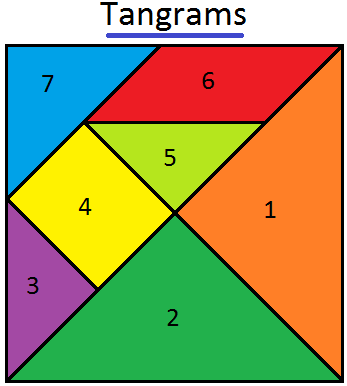
Tangrams Math | Traditional Chinese Geometrical Puzzle | Triangles
Apr 18, 24 12:31 AM
Tangram is a traditional Chinese geometrical puzzle with 7 pieces (1 parallelogram, 1 square and 5 triangles) that can be arranged to match any particular design. In the given figure, it consists of o…