Subscribe to our ▶️YouTube channel🔴 for the latest videos, updates, and tips.
Home | About Us | Contact Us | Privacy | Math Blog
Speed Distance and Time
Can you tell which moves faster - a motorcycle or a bicycle? Certainly, a motorcycle, because a motorcycle can cover longer distance in shorter time. In other words, we can say, a motorcycle runs at a greater speed than a bicycle.
For knowing how fast an object moves, we consider the distance travelled by it and the time taken in travelling the distance.
The distance travelled in a unit time by an object is called its speed.
Speed is the distance covered by an object in a unit time.
Speed = DistanceTime
From the above formula, we can derive the following relationship.
Time = DistanceSpeed
Distance = Time x Speed
If we represent speed by S, Distance by D and Time by T, we can express the relationship between them as follows.
S = DT
T = DS
D = T x S
We measure speed in kilometres per hour (km/hr) metres per minute (m/min) or metres per second (m/sec).
Suppose an Express train leaves the station A at 0900 hours. It runs nonstop and reaches the station B at 1100 hours. So the Express train take 2 hours to cover the distance. A Mail train covers the distance between these stations in 3 hours. If the distance between the two stations is 120 km, which train travels faster?
To find this, we use the unitary method.
The distance covered by the Express train in 2 hours = 120 km
The distance covered by the Express train in 1 hour = 1202 km = 60 km
The distance covered by the Mail train in 3 hours = 120 km
The distance covered by the Mail train in 1 hour = 1203 km = 40 km
So, the Express train travels more distance than the Mail train in 1 hour. Hence, the Express train travels faster than the Mail train. We say that the Express train has greater speed than the Mail train.
Speed: The distance travelled by a body or vehicle in a unit time is known as its speed.
Speed = Distance (in unit of length)Time (in unit of time)
Average Speed: The total distance covered by a body divided by the total time taken by the body is known as average speed.
Average Speed = Total distance travelledTotal Time Taken
and Speed = Total Distance CoveredTotal time taken-time of stoppage
= DistanceTime
If there is no stoppage, that is, the time of stoppage is zero, the average speed equals the speed.
Solved Examples on Speed Distance and Time:
1. Nancy travelled a distance of 455 km by car in 10
hours. Find the speed of the car.
Distance travelled by car = 455 km
Time taken = 10 hours
Therefore, speed = DistanceTime
= 45510 km/hr
= 45.5 km per hour
2. Find the speed and average speed of a train which leaves Madras at 1 p.m. and reaches Vijayawada in the same day at 9 p.m. The distance between the two stations is 432 km and the total time for stoppage is 2 hours between these stations.
Total time taken = 9 -1, that is, 8 hours;
Time of stoppage = 2 hours, that is, actual time taken = 8 hours - 2 hours = 6 hours
Speed = DistanceTime
= 432km6hr
= 4326
= 72 km/hr
Average speed = Total DistanceTotal Time
= 4328 km/hr
= 54 km/hr
3. A car travels a distance of 595 km in 8 ½ hours. What is its speed?
Distance travelled = 595 km
Time taken to travel this distance = 812 hours = 172 hours
Speed of the car = DistanceTime
= 595172 km/hour
= 592×217
= 70 km/hr
Therefore, the speed of the car = 70 km/hour.
4. A train covers a distance of 1417 km in 13 hours. Find the speed of the train.
Solution:
Distance = 1417 km
Time taken = 13 hours
Speed = DistanceTime
= 1417km13hr
= 109 km/hr.
5. A car is moving at a speed of 69 km/hr. Find the time taken by the car to cover a distance of 1173 km.
Solution:
Distance = 1173 km
Speed = 69 km/hr
Time = DistanceSpeed
= 1173km69km/hr
= 9 hrs.
Note: km ÷ kmhr
= km × hrk̸m
= hr
6. A bus travels a speed of 59 km/hr. Find the distance covered by it in 7 hours.
Solution:
Speed = 59 km/hr
Time = 7 hrs
Distance = Speed × Time
= 59 km/hr × 7 hrs
= 413 km
Note: kmh̸r × hr
= km
7. A motorbike running at a speed of 63 km/hr. How many kilometres will it cover in in 523 hours?
Solution:
Speed = 63 km/hr.
Time = 523 hrs = 173 hrs
Distance = Speed × Time
= 63 km/hr × 173 hr
= 63km/hr×17hr3
= 357 km
Note: kmh̸r × hr
= km
Average Speed:
Sometimes, the speed of a moving object varies from time to time. In such cases, we calculate the average speed of the moving object.
Let us consider an example.
8. A train covers 86 km in the 1st hour, 90 km in the 2nd hour, 80 km in the 3rd hour and 84 km in the 4th hour. Find the average speed of the train.
Solution:
Total distance covered = 86 km + 90 km + 80 km + 84 km
= 340 km
Total time taken = 4 hours
Average speed = \(\frac{\textrm{Distance}}{\textrm{Time}}\)
= 340km4
= 85 km/hr
Worksheet on Speed Distance and Time
I. Calculate the speed in each case.
|
1 Distance = 800 km 2. Distance = 12000 m 3. Distance = 252 cm 4. Distance = 600 cm 5. Distance = 950 m |
Time = 6 hours Time = 80 minutes Time = 6 seconds Time = 8 seconds Time = 10 minutes |
Answer:
I: 1. 133.34 km/hr
2. 150 m/min
3. 42 cm/sec
4. 75 cm/sec
5. 95 m/min
II. Calculate the distance covered in each case.
|
1. Speed = 182 km/hr 2. Speed = 20.5 m/min 3. Speed = 60 cm/sec 4. Speed = 40 km/hr 5. Speed = 80 km/hr |
Time = 1 hour 20 minutes Time = 2 hours 30 minutes Time = 16 seconds Time = 1 hour Time = 2 hours |
Answer:
II: 1. 242.67 km
2. 3075 metre
3. 960 cm
4. 40 km
5. 160 km
III. Calculate the time taken in each case.
|
1. Distance = 1400 km 2. Distance = 3760 km 3. Distance = 30 m 4. Distance = 160 m 5. Distance = 1200 km |
Speed = 200 km/hr Speed = 90 km/hr Speed = 60 cm/sec Speed = 40 m/sec Speed = 60 km/hr |
Answer:
III: 1. 7 hrs
2. 41.78 hrs
3. 50 sec
4. 40 sec
5. 20 hrs
Express Speed in Different Units
To find Speed when Distance and Time are given.
To find the Distance when Speed and Time are given.
To find Time when Distance and Speed are given.
Worksheet on Expressing Speed in Different Units
Worksheet on Speed, Distance and Time.
5th Grade Numbers Page
5th Grade Math Problems
From Speed Distance and Time to HOME PAGE
Didn't find what you were looking for? Or want to know more information about Math Only Math. Use this Google Search to find what you need.
Recent Articles
-
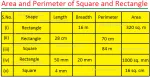
Worksheet on Area of a Square and Rectangle | Area of Squares & Rectan
Jul 19, 25 05:00 AM
We will practice the questions given in the worksheet on area of a square and rectangle. We know the amount of surface that a plane figure covers is called its area. 1. Find the area of the square len… -
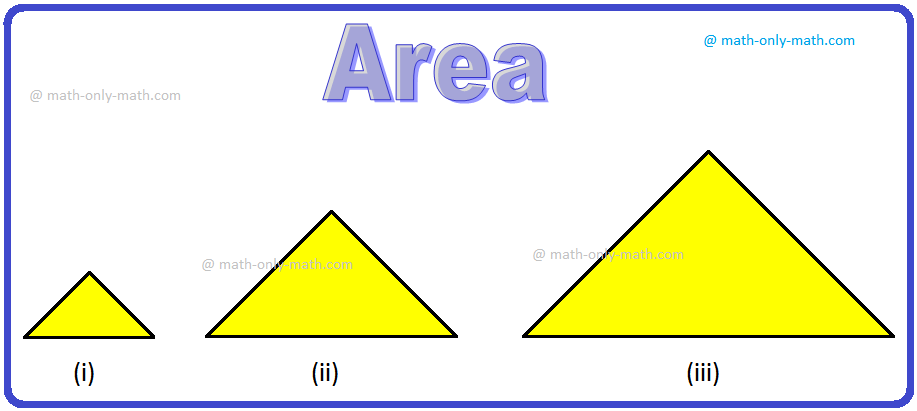
Area of Rectangle Square and Triangle | Formulas| Area of Plane Shapes
Jul 18, 25 10:38 AM
Area of a closed plane figure is the amount of surface enclosed within its boundary. Look at the given figures. The shaded region of each figure denotes its area. The standard unit, generally used for… -
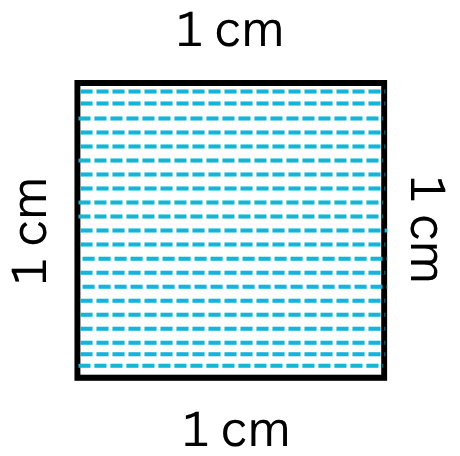
What is Area in Maths? | Units to find Area | Conversion Table of Area
Jul 17, 25 01:06 AM
The amount of surface that a plane figure covers is called its area. It’s unit is square centimeters or square meters etc. A rectangle, a square, a triangle and a circle are all examples of closed pla… -
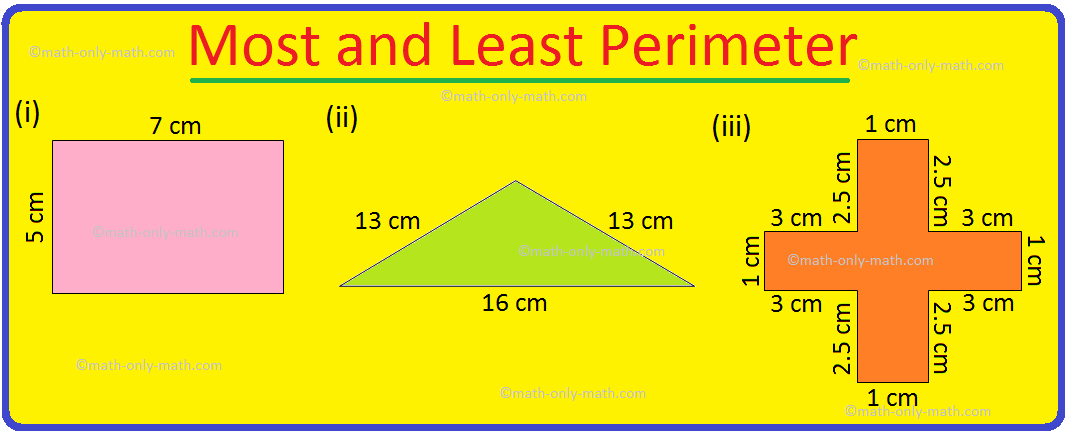
Worksheet on Perimeter | Perimeter of Squares and Rectangle | Answers
Jul 17, 25 12:40 AM
Practice the questions given in the worksheet on perimeter. The questions are based on finding the perimeter of the triangle, perimeter of the square, perimeter of rectangle and word problems. I. Find… -
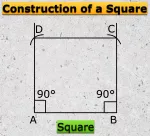
Formation of Square and Rectangle | Construction of Square & Rectangle
Jul 16, 25 11:46 PM
In formation of square and rectangle we will learn how to construct square and rectangle. Construction of a Square: We follow the method given below. Step I: We draw a line segment AB of the required…









New! Comments
Have your say about what you just read! Leave me a comment in the box below. Ask a Question or Answer a Question.