sin θ = sin ∝
How to find the general solution of an equation of the form sin θ = sin ∝?
Prove that the general solution of sin θ = sin ∝ is given by θ = nπ + (-1)\(^{n}\) ∝, n ∈ Z.
Solution:
We have,
sin θ = sin ∝
⇒ sin θ - sin ∝ = 0
⇒ 2 cos \(\frac{θ + ∝}{2}\) sin \(\frac{θ - ∝}{2}\) = 0
Therefore either cos \(\frac{θ + ∝}{2}\) = 0 or, sin \(\frac{θ - ∝}{2}\) = 0
Now, from cos \(\frac{θ + ∝}{2}\) = 0 we
get, \(\frac{θ + ∝}{2}\) = (2m + 1)\(\frac{π}{2}\), m ∈ Z
⇒ θ = (2m + 1)π - ∝, m ∈ Z i.e., (any odd multiple of π) - ∝ ……………….(i)
And from sin \(\frac{θ - ∝}{2}\) = 0 we get,
\(\frac{θ - ∝}{2}\) = mπ, m ∈ Z
⇒ θ = 2mπ + ∝, m ∈ Z i.e., (any even multiple of π) + ∝ …………………….(ii)
Now combining the solutions (i) and (ii) we get,
θ = nπ + (-1)\(^{n}\) ∝, where n ∈ Z.
Hence, the general solution of sin θ = sin ∝ is θ = nπ + (-1)\(^{n}\) ∝, where n ∈ Z.
Note: The equation csc θ = csc ∝ is equivalent to sin θ = sin ∝ (since, csc θ = \(\frac{1}{sin θ}\) and csc ∝ = \(\frac{1}{sin ∝}\)). Thus, csc θ = csc ∝ and sin θ = sin ∝ have the same general solution.
Hence, the general solution of csc θ = csc ∝ is θ = nπ + (-1)\(^{n}\) ∝, where n ∈ Z.
1. Find the general values of x which satisfy the equation sin 2x = -\(\frac{1}{2}\)
solution:
sin 2x = -\(\frac{1}{2}\)
sin 2x = - sin \(\frac{π}{6}\)
⇒ sin 2x = sin (π + \(\frac{π}{6}\))
⇒ sin 2x = sin \(\frac{7π}{6}\)
⇒ 2x = nπ + (-1)\(^{n}\) \(\frac{7π}{6}\), n ∈ Z
⇒ x = \(\frac{nπ}{2}\) + (-1)\(^{n}\) \(\frac{7π}{12}\), n ∈ Z
Therefore the general solution of sin 2x = -\(\frac{1}{2}\) is x = \(\frac{nπ}{2}\) + (-1)\(^{n}\) \(\frac{7π}{12}\), n ∈ Z
2. Find the general solution of the trigonometric equation sin 3θ = \(\frac{√3}{2}\).
Solution:
sin 3θ = \(\frac{√3}{2}\)
⇒ sin 3θ = sin \(\frac{π}{3}\)
⇒ 3θ = = nπ + (-1)\(^{n}\) \(\frac{π}{3}\), where, n = 0, ± 1, ± 2, ± 3, ± 4 .....
⇒ θ = \(\frac{nπ}{3}\) + (-1)\(^{n}\) \(\frac{π}{9}\),where, n = 0, ± 1, ± 2, ± 3, ± 4 .....
Therefore the general solution of sin 3θ = \(\frac{√3}{2}\) is θ = \(\frac{nπ}{3}\) + (-1)\(^{n}\) \(\frac{π}{9}\), where, n = 0, ± 1, ± 2, ± 3, ± 4 .....
3. Find the general solution of the equation csc θ = 2
Solution:
csc θ = 2
⇒ sin θ = \(\frac{1}{2}\)
⇒ sin θ = sin \(\frac{π}{6}\)
⇒ θ = nπ + (-1)\(^{n}\) \(\frac{π}{6}\), where, n ∈ Z, [Since, we know that the general solution of the equation sin θ = sin ∝ is θ = 2nπ + (-1)\(^{n}\) ∝, where n = 0, ± 1, ± 2, ± 3, ……. ]
Therefore the general solution of csc θ = 2 is θ = nπ + (-1)\(^{n}\) \(\frac{π}{6}\), where, n ∈ Z
4. Find the general solution of the trigonometric equation sin\(^{2}\) θ = \(\frac{3}{4}\).
Solution:
sin\(^{2}\) θ = \(\frac{3}{4}\).
⇒ sin θ = ± \(\frac{√3}{2}\)
⇒ sin θ = sin (± \(\frac{π}{3}\))
⇒ θ = nπ + (-1)\(^{n}\) ∙ (±\(\frac{π}{3}\)), where, n ∈ Z
⇒ θ = nπ ±\(\frac{π}{3}\), where, n ∈ Z
Therefore the general solution of sin\(^{2}\) θ = \(\frac{3}{4}\) is θ = nπ ±\(\frac{π}{3}\), where, n ∈ Z
- General solution of the equation sin x = ½
- General solution of the equation cos x = 1/√2
- General solution of the equation tan x = √3
- General Solution of the Equation sin θ = 0
- General Solution of the Equation cos θ = 0
- General Solution of the Equation tan θ = 0
- General Solution of the Equation sin θ = sin ∝
- General Solution of the Equation sin θ = 1
- General Solution of the Equation sin θ = -1
- General Solution of the Equation cos θ = cos ∝
- General Solution of the Equation cos θ = 1
- General Solution of the Equation cos θ = -1
- General Solution of the Equation tan θ = tan ∝
- General Solution of a cos θ + b sin θ = c
- Trigonometric Equation Formula
- Trigonometric Equation using Formula
- General solution of Trigonometric Equation
- Problems on Trigonometric Equation
11 and 12 Grade Math
From sin θ = sin ∝ to HOME PAGE
Didn't find what you were looking for? Or want to know more information about Math Only Math. Use this Google Search to find what you need.
Recent Articles
-
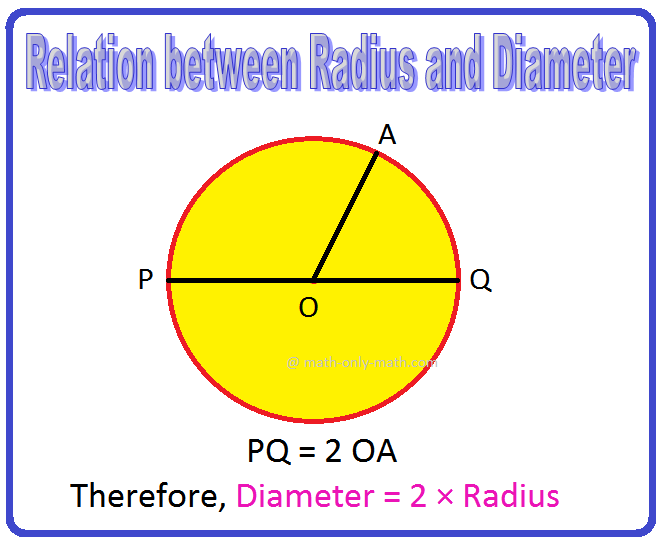
Relation between Diameter Radius and Circumference |Problems |Examples
Apr 22, 24 05:19 PM
Relation between diameter radius and circumference are discussed here. Relation between Diameter and Radius: What is the relation between diameter and radius? Solution: Diameter of a circle is twice -
Circle Math | Terms Related to the Circle | Symbol of Circle O | Math
Apr 22, 24 01:35 PM
In circle math the terms related to the circle are discussed here. A circle is such a closed curve whose every point is equidistant from a fixed point called its centre. The symbol of circle is O. We… -
Preschool Math Activities | Colorful Preschool Worksheets | Lesson
Apr 21, 24 10:57 AM
Preschool math activities are designed to help the preschoolers to recognize the numbers and the beginning of counting. We believe that young children learn through play and from engaging -
Months of the Year | List of 12 Months of the Year |Jan, Feb, Mar, Apr
Apr 20, 24 05:39 PM
There are 12 months in a year. The months are January, February, march, April, May, June, July, August, September, October, November and December. The year begins with the January month. December is t… -
What are Parallel Lines in Geometry? | Two Parallel Lines | Examples
Apr 20, 24 05:29 PM
In parallel lines when two lines do not intersect each other at any point even if they are extended to infinity. What are parallel lines in geometry? Two lines which do not intersect each other