Simplification of Numerical Expressions
We will discuss here about the simplification of numerical expressions. We know how to perform the four fundamental operations, that is namely, addition, subtraction, multiplication and division involving whole numbers, fractional numbers and decimals. We perform only one operation at a time. Now we will learn how to perform two or more operations together.
To simplify a numerical expression having two or more operations, we perform operation like: Division first, followed by Multiplication, Addition and then Subtraction. A standard result called BODMAS is applied for simplification of these operations.
The word BODMAS stands for:
B → Brackets
O → of means (Multiplication ×)
D → Division
M → Multiplication
A → Addition
S → Subtraction
If the brackets are present in the problem, we first
simplify the brackets. There are four kind of brackets.
1. ( ) → simple brackets or round brackets or parenthesis.
2. { } → Braces or Curly brackets.
3. [ ] → Square brackets.
4. ______ → This is a line called bar, vinculum. If two or more types of brackets are involved in the problem, then they are removed in this order ‘_________’, ( ), { }, [ ].
Solved examples to simplify the numerical expressions:
Simplify the following:
(i) [12 + {7 - (8 ÷ 2)}] × 3
= [12 + {7 - 4}] × 3 (Round brackets removed)
= [12 + 3] × 3 (Curly brackets removed)
= 15 × 3 (Square brackets removed)
= 45
(ii) 14 + [22 - {8 + (6 ÷ 2)}]
= 14 + [22 - {8 + 3}] (Round brackets removed)
= 14 + [22 - 11] (Curly brackets removed)
= 14 + 11 (Square brackets removed)
= 25
From Simplification of Numerical Expressions to HOME PAGE
Didn't find what you were looking for? Or want to know more information about Math Only Math. Use this Google Search to find what you need.
Recent Articles
-
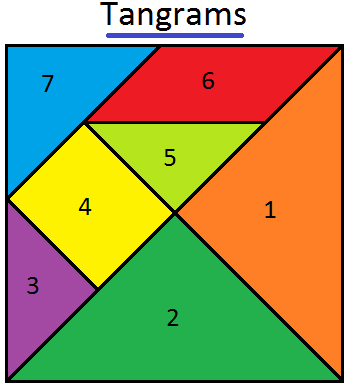
Tangrams Math | Traditional Chinese Geometrical Puzzle | Triangles
Apr 17, 24 01:53 PM
Tangram is a traditional Chinese geometrical puzzle with 7 pieces (1 parallelogram, 1 square and 5 triangles) that can be arranged to match any particular design. In the given figure, it consists of o… -
Time Duration |How to Calculate the Time Duration (in Hours & Minutes)
Apr 17, 24 01:32 PM
We will learn how to calculate the time duration in minutes and in hours. Time Duration (in minutes) Ron and Clara play badminton every evening. Yesterday, their game started at 5 : 15 p.m. -
Worksheet on Third Grade Geometrical Shapes | Questions on Geometry
Apr 16, 24 02:00 AM
Practice the math worksheet on third grade geometrical shapes. The questions will help the students to get prepared for the third grade geometry test. 1. Name the types of surfaces that you know. 2. W… -
4th Grade Mental Math on Factors and Multiples |Worksheet with Answers
Apr 16, 24 01:15 AM
In 4th grade mental math on factors and multiples students can practice different questions on prime numbers, properties of prime numbers, factors, properties of factors, even numbers, odd numbers, pr… -
Worksheet on Factors and Multiples | Find the Missing Factors | Answer
Apr 15, 24 11:30 PM
Practice the questions given in the worksheet on factors and multiples. 1. Find out the even numbers. 27, 36, 48, 125, 360, 453, 518, 423, 54, 58, 917, 186, 423, 928, 358 2. Find out the odd numbers.