Reflection of a Point in y-axis

How to find the co-ordinates of the reflection of a point in y-axis?

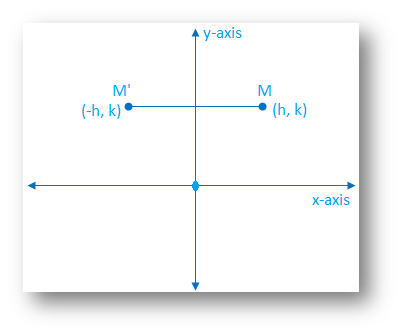
To find the co-ordinates in the adjoining figure, y-axis represents the plane mirror. M is the any point whose co-ordinates are (h, k) in the rectangular axes in first quadrant.

Observe when point M is reflected in y-axis, the image M' is formed in the second quadrant whose co-ordinates are (-h, k).

Thus we conclude that when a point is reflected in y-axis, then the y-co-ordinate remains same and then x-co-ordinate become negative.

Thus, the image of M (h, k) is M' (-h, k).

Rules to find the reflection of a point in the y-axis:

(i) Change the sign of abscissa i.e., x-coordinate.

(ii) Retain the ordinate i.e., y-coordinate.

Examples to find the co-ordinates of the reflection of a point in y-axis:

1. Write the co-ordinates of the image of the following points when reflected in y-axis.

(i) (-4 , 3)            

(ii) (3, 5)             

(iii) (-1, -6)                               

(iv) (5, -7)

Solution:

(i) The image of (-4 , 3) is (4 , 3).

(ii) The image of (3, 5) is (-3, 5).

(iii) The image of (-1 , -6) is (1, -6).

(iv) The image of (5, -7) is (-5, -7).

2. Find the reflection of the following in y-axis.

(i) P (-7, 9)

(ii) Q (-3, -6)

(iii) R (4, 8)

(iv) S (5, -7)

Solution:

(i) The image of P (-7, 9) is P' (7, 9).

(ii) The image of Q (-3, -6) is Q' (3, -6).

(iii) The image of R (4, 8) is R' (-4, 8).

(iv) The image of S (5, -7) is S' (-5, -7).

Solved example to find the reflection of a parallelogram in y-axis:

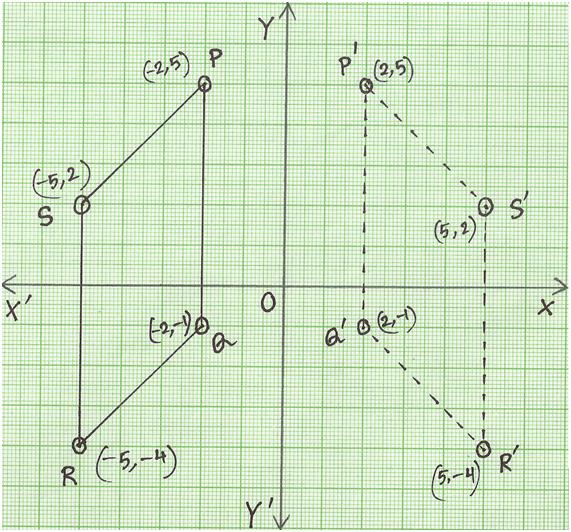
3. Draw the image of the parallelogram PQRS having its vertices P (-2, 5); Q (-2, -1); R (-5, -4); S (-5, 2) in y-axis.

Solution:

Plot the points P (-2, 5); Q (-2, -1); R (-5, -4); S (-5, 2) on the graph paper. Now join PQ, QR, RS and SP to get a parallelogram.

When reflected in y-axis, we get P' (2, 5); Q' (2, -1); R' (5, -4); S' (5, 2). Now join P'Q', Q'R', R'S' and S'P'.

Thus we get the parallelogram P'Q'R'S as the image of the parallelogram  PQRS in y-axis.

Solved example to find the reflection of a rectangle in y-axis:

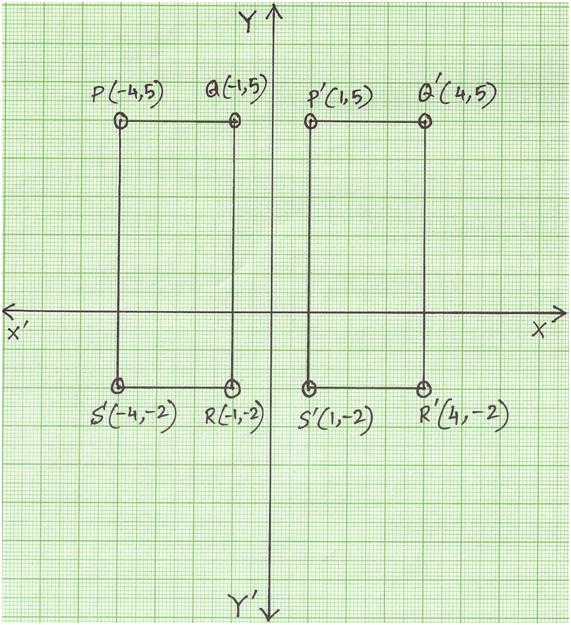
4. The co-ordinate of the rectangle PQRS having its vertices P (-4, 5), Q (-1, 5), R (-1, -2), S (-4, -2). Draw the image of the figure when reflected in y-axis.

Solution:

Plot the co-ordinates of the points  P (-4, 5), Q (-1, 5), R (-1, -2), S (-4, -2) on the graph paper.

Join PQ, QR, RS and SP to get a rectangle.

When reflected in y-axis we get;

The image of P (-4, 5) is P' (4, 5)

The image of Q (-1, 5) is Q' (1, 5)

The image of R (-1, -2) is R' (1, -2)

The image of S (-4, -2) is R' (4, -2)

Plot the point P', Q', R' and S' on the same graph paper. Now join P'Q', Q'R', R'S' and S'P'.

Thus we get the rectangle P'Q'R'S as the image of the rectangle PQRS when reflection in y-axis.

Note: Point M (h, k) has its image M' (-h, k) when reflected in y-axis.

Thus, we conclude that when the reflection of a point in y-axis:

• y-axis acts as a plane mirror.

• M is the point whose co-ordinates are (h, k).

• The image of M i.e. M' lies in second quadrant.

• The co-ordinates of M' are (-h, k).
  

● Related Concepts

● Lines of Symmetry

● Point Symmetry

● Rotational Symmetry

● Order of Rotational Symmetry

● Types of Symmetry

● Reflection

● Reflection of a Point in x-axis

● Reflection of a point in origin

● Rotation

● 90 Degree Clockwise Rotation

● 90 Degree Anticlockwise Rotation

● 180 Degree Rotation

7th Grade Math Problems

8th Grade Math Practice

From Reflection of a Point in y-axis to HOME PAGE