Problems on Surds
We will solve different types of problems on surds.
1. State whether the following are surds or not with reasons:
(i) √5 × √10
(ii) √8 × √6
(iii) √27 × √3
(iv) √16 × √4
(v) 5√8 × 2√6
(vi) √125 × √5
(vii) √100 × √2
(viii) 6√2 × 9√3
(ix)
√120 × √45
(x) √15 × √6
(xi) ∛5 × ∛25
Solution:
(i) √5 × √10
= \(\sqrt{5\cdot 10}\)
= \(\sqrt{5\cdot 5\cdot 2}\)
= 5√2, which is an irrational number. Hence, it is a surd.
(ii) √8 × √6
= \(\sqrt{8\cdot 6}\)
= \(\sqrt{2\cdot 2\cdot 2\cdot 2\cdot 3}\)
= 4√3, which is an irrational number. Hence, it is a surd.
(iii) √27 × √3
= \(\sqrt{27\cdot 3}\)
= \(\sqrt{3\cdot 3\cdot 3\cdot 3}\)
= 3 × 3
= 9, which is a rational number. Hence, it is not a surd.
(iv) √16 × √4
= \(\sqrt{16\cdot 4}\)
= \(\sqrt{2\cdot 2\cdot 2\cdot 2\cdot 2\cdot 2}\)
= 2 × 2 × 2
= 8, which is a rational number. Hence, it is not a surd.
(v) 5√8 × 2√6
= 5 × 2 \(\sqrt{2\cdot 2\cdot 2\cdot 2\cdot 3}\)
= 10 × 2 × 2 × √3
= 40√3, which is an irrational number. Hence, it is a surd.
(vi) √125 × √5
= \(\sqrt{125\cdot 5}\)
= \(\sqrt{5\cdot 5\cdot 5\cdot 5}\)
= 5 × 5
= 25, which is a rational number. Hence, it is not a surd.
(vii) √100 × √2
= \(\sqrt{100\cdot 2}\)
= \(\sqrt{2\cdot 2\cdot 5\cdot 5\cdot 2}\)
= 2 × 5 × √2
= 10√2, which is an irrational number. Hence, it is a surd.
(viii) 6√2 × 9√3
= 6 × 9 \(\sqrt{2\cdot 3}\)
= 54 × √6
= 54√6, which is an irrational number. Hence, it is a surd.
(ix) √120 × √45
= \(\sqrt{120\cdot 45}\)
= \(\sqrt{2\cdot 2\cdot 2\cdot 3\cdot 5\cdot 3\cdot 3\cdot 5}\)
= 2 × 3 × 5 × √6
= 30√6, which is an irrational number. Hence, it is a surd.
(x) √15 × √6
= \(\sqrt{15\cdot 6}\)
= \(\sqrt{3\cdot 5\cdot 2\cdot 3}\)
= 3√10, which is an irrational number. Hence, it is a surd.
(xi) ∛5 × ∛25
= \(\sqrt[3]{5 × 25}\)
= \(\sqrt[3]{5 × 5 × 5}\)
= 5, which is a rational number. Hence, it is not a surd.
2. Rationalize the denominator of the surd \(\frac{√5}{3√3}\).
Solution:
\(\frac{√5}{3√3}\)
= \(\frac{√5}{3√3}\) × \(\frac{√3}{√3}\)
= \(\frac{\sqrt{5 \times 3}}{3 \times \sqrt{3 \times 3}}\)
= \(\frac{√15}{3 × 3}\)
= \(\frac{1}{9}\)√15
3. Rationalize the denominator of the surd \(\frac{2}{√7 - √3}\)
Solution:
\(\frac{2}{√7 - √3}\)
= \(\frac{2 × (√7 + √3)}{(√7 - √3) × (√7 + √3)}\)
= \(\frac{2 (√7 + √3)}{7 - 3}\)
= \(\frac{2 (√7 + √3)}{4}\)
= \(\frac{(√7 + √3)}{2}\)
4. Express the surd \(\frac{√3}{5√2}\) in the simplest form.
Solution:
\(\frac{√3}{5√2}\)
= \(\frac{√3}{5√2}\) × \(\frac{√2}{√2}\)
= \(\frac{\sqrt{3 \times 2}}{5 \times \sqrt{2 \times 2}}\)
= \(\frac{√6}{5 × 2}\)
= \(\frac{1}{10}\)√6, is the required simplest form of the given surd.
5. Expand (2√2 - √6)(2√2 + √6), expressing the result in the simplest form of surd:
Solution:
(2√2 - √6)(2√2 + √6)
= (2√2)\(^{2}\) - (√6)\(^{2}\), [Since, (x + y)(x - y) = x\(^{2}\) - y\(^{2}\)]
= 8 - 6
= 2
6. Fill in the blanks:
(i) Surds having the same irrational factors are called ____________ surds.
(ii) √50 is a surd of order ____________.
(iii) \(\sqrt[9]{19}\) × \(\sqrt[5]{10^{0}}\) = ____________.
(iv) 6√5 is a ____________ surd.
(v) √18 is a ____________ surd.
(vi) 2√7 + 3√7 = ____________.
(vii) The order of the surd 3∜5 is a ____________.
(viii) ∛4 × ∛2 in the simplest form is = ____________.
Solution:
(i) similar.
(ii) 2
(iii) \(\sqrt[9]{19}\), [Since, we know, 10\(^{0}\) = 1]
(iv) mixed
(v) pure
(vi) 5√7
(vii) 4
(viii) 2
11 and 12 Grade Math
From Problems on Surds to HOME PAGE
Didn't find what you were looking for? Or want to know more information about Math Only Math. Use this Google Search to find what you need.
Recent Articles
-
Symmetrical Shapes | One, Two, Three, Four & Many-line Symmetry
Apr 23, 24 04:50 PM
Symmetrical shapes are discussed here in this topic. Any object or shape which can be cut in two equal halves in such a way that both the parts are exactly the same is called symmetrical. The line whi… -
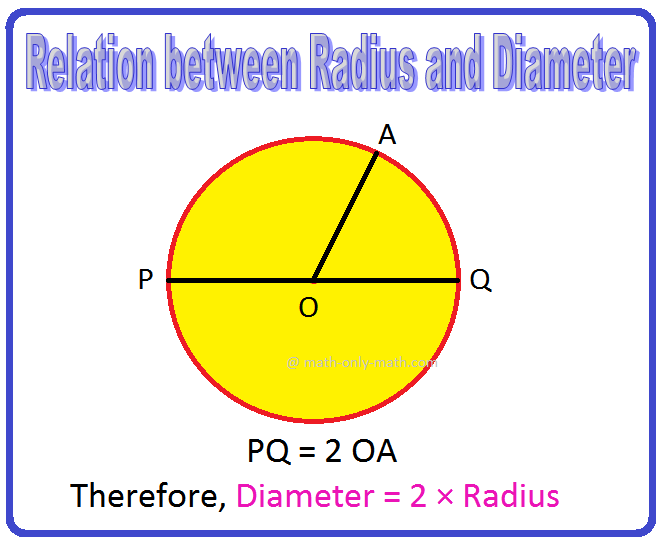
Relation between Diameter Radius and Circumference |Problems |Examples
Apr 23, 24 03:15 PM
Relation between diameter radius and circumference are discussed here. Relation between Diameter and Radius: What is the relation between diameter and radius? Solution: Diameter of a circle is twice -
Circle Math | Terms Related to the Circle | Symbol of Circle O | Math
Apr 22, 24 01:35 PM
In circle math the terms related to the circle are discussed here. A circle is such a closed curve whose every point is equidistant from a fixed point called its centre. The symbol of circle is O. We… -
Preschool Math Activities | Colorful Preschool Worksheets | Lesson
Apr 21, 24 10:57 AM
Preschool math activities are designed to help the preschoolers to recognize the numbers and the beginning of counting. We believe that young children learn through play and from engaging -
Months of the Year | List of 12 Months of the Year |Jan, Feb, Mar, Apr
Apr 20, 24 05:39 PM
There are 12 months in a year. The months are January, February, march, April, May, June, July, August, September, October, November and December. The year begins with the January month. December is t…