Problems on Compound Angles
We will learn how to solve different types of problems on compound angles using formula.
We will see step-by-step how to deal with the trigonometrical ratios of compound angles in different questions.
1. An angle θ is divided into two parts so that the ratio of the tangents of the parts is k; if the difference between the parts be ф, prove that, sin ф = (k - 1)/(k + 1) sin θ .
Solution:
Let, α and β be the two parts of the angle θ.
Therefore, θ = α + β.
By question, θ = α - β. (assuming a >β)
and tan α/tan β = k
⇒ sin α cos β/sin β cos α = k/1
⇒ (sin α cos β + cos α sin β)/(sin α cos β - cos α sin β) = (k + 1)/(k - 1), [by componendo and dividendo]
⇒ sin (α + β)/sin (α - β) = (k + 1)/(k - 1)
⇒ (k + 1) sin Ø = (k - 1) sin θ, [Since we know that α + β = θ; α + β = ф]
⇒ sin ф = (k - 1)/(k + 1) sin θ. Proved.
2. If x + y = z and
tan x = k tan y, then prove that sin (x - y) = [(k - 1)/(k + 1)] sin z
Solution:
Given tan x = k tan y
⇒ sin x/cos x = k ∙ sin y/cos y
⇒ sin x cos y/cos x sin y = k/1
Applying componendo and dividend, we get
sin x cos y + cos x sin y/ sin x cos y - cos x sin y = k + 1/k - 1
⇒ sin (x + y)/sin (x – y) = k + 1/k - 1
⇒ sin z/sin (x – y) = k + 1/k - 1, [Since x + y = z given]
⇒ sin (x – y) = [k + 1/k – 1] sin z Proved.
3. If A + B + C = π and cos A = cos B cos C, show that, tan B tan C = 2
Solution:
A + B + C = π
Therefore, B + C = π - A
⇒ cos (B + C) = cos (π - A)
⇒ cos B cos C - sin B sin C = - cos A
⇒ cos B cos C + cos B cos C = sin B sin C,[Since we know, cos A = cos B cos C]
⇒ 2 cos B cos C = sin B sin C
⇒ tan B tan C = 2 Proved.
Note: In different problems on compound angles we need to use the formula as required.
4. Prove that cot 2x + tan x = csc 2x
Solution:
L.H.S. = cot 2x + tan x
= cos 2x/sin 2x + sin x/cos x
= cos 2x cos x + sin 2x sin x/sin 2x cos x
= cos (2x - x)/sin 2x cos x
= cos x/sin 2x cos x
= 1/sin 2x
= csc 2x = R.H.S. Proved.
5. If sin (A + B) + sin (B + C) + cos (C - A) = -3/2 show that,
sin A + cos B + sin C = 0; cos A + sin B + cos C = 0.
Solution:
Since, sin (A + B) + sin (B + C) + cos (C - A) = -3/2
Therefore, 2 (sin A cos B + cos A sin B + sin B cos C + cos B sin C + cos C cos A + sin C sin A) = -3
⇒ 2 (sin A cos B + cos A sin B + sin B cos C + cos B sin C + cos C cos A + sin C sin A) = - (1 + 1 + 1)
⇒ 2 (sin A cos B + cos A sin B + sin B cos C + cos B sin C + cos C cos A + sin C sin A) = - [(sin^2 A + cos^2 A) + (sin^2 B + cos^2 B) + (sin^2 C + cos^2 C)]
⇒ (sin^2 A + cos^2 B + sin^2 C + 2 sin A sin C + 2 sin A cos B + 2 cos B sin C) + (cos^2 A + sin^2 B + cos^2 C + 2 cos A sin B + 2 sin B cos C + 2 cos A cos C) = 0
⇒ (sin A + sin B + sin C)^2 + (cos A + sin B + cos C)^2
Now the sum of squares of two real quantities is zero if each quantity is separately zero.
Therefore, sin A + cos B + Sin C = 0
and cos A + sin B + cos C = 0. Proved.
11 and 12 Grade Math
From Problems on Compound Angles to HOME PAGE
Didn't find what you were looking for? Or want to know more information about Math Only Math. Use this Google Search to find what you need.
Recent Articles
-
Symmetrical Shapes | One, Two, Three, Four & Many-line Symmetry
Apr 23, 24 04:50 PM
Symmetrical shapes are discussed here in this topic. Any object or shape which can be cut in two equal halves in such a way that both the parts are exactly the same is called symmetrical. The line whi… -
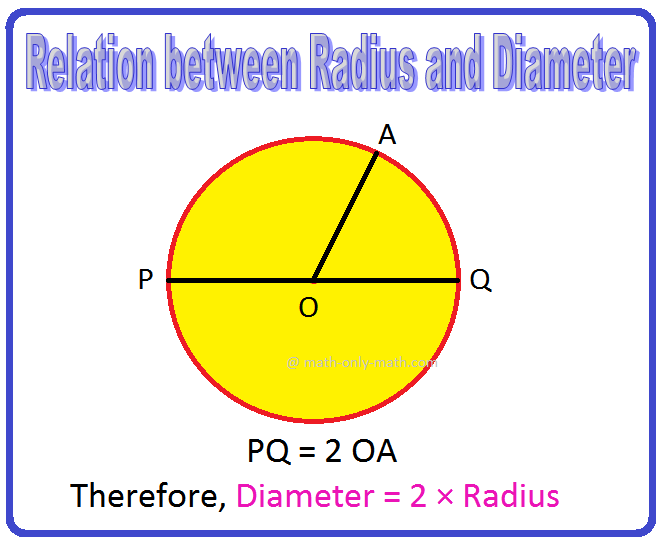
Relation between Diameter Radius and Circumference |Problems |Examples
Apr 23, 24 03:15 PM
Relation between diameter radius and circumference are discussed here. Relation between Diameter and Radius: What is the relation between diameter and radius? Solution: Diameter of a circle is twice -
Circle Math | Terms Related to the Circle | Symbol of Circle O | Math
Apr 22, 24 01:35 PM
In circle math the terms related to the circle are discussed here. A circle is such a closed curve whose every point is equidistant from a fixed point called its centre. The symbol of circle is O. We… -
Preschool Math Activities | Colorful Preschool Worksheets | Lesson
Apr 21, 24 10:57 AM
Preschool math activities are designed to help the preschoolers to recognize the numbers and the beginning of counting. We believe that young children learn through play and from engaging -
Months of the Year | List of 12 Months of the Year |Jan, Feb, Mar, Apr
Apr 20, 24 05:39 PM
There are 12 months in a year. The months are January, February, march, April, May, June, July, August, September, October, November and December. The year begins with the January month. December is t…