Subscribe to our ▶️YouTube channel🔴 for the latest videos, updates, and tips.
Home | About Us | Contact Us | Privacy | Math Blog
Polar Co-ordinates
What is Polar Co-ordinates?
Besides Cartesian co-ordinate system we have several other methods for locating position of a point on a plane. Of all these system we shall make here a brief discussion on Polar Co-ordinates only. Polar Co-ordinates are widely used in higher mathematics as well as in other branches of science.
In polar co-ordinate system the position of a point on the reference plane is uniquely determined referred to a fixed point on the plane and a half line drawn through the fixed point. The fixed point is called the Pole or Origin and the half line drawn through the pole is called the Initial Line.
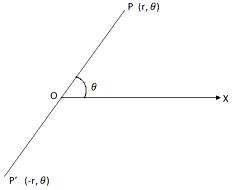
Let OX be the initial line drawn through the pole O on the plane of reference. Take any point P on the plane and join OP .
If OP = r and ∠XOP = θ then the real numbers r and θ are together called the Polar Co-ordinates of P and denoted by (r, θ); here OP. If OP = r and Polar Co-ordinates of P and denoted by (r, θ); here OP = r is called the Radius Vector and ∠XOP = θ, the Vectorial Angle of P. the angle θ is measured by the method of measurement of trigonometrical angle i.e., θ is taken to be positive when it is measured in the anti-clockwise sense from the initial line and negative when it is measured in the clockwise sense from the initial line.
By convection, to represent the polar co-ordinate of a point we first write the radius vector (r) and then the vectorial angle (θ) and they are put together in braces putting a comma between them.
Note:
(i) for given values of r and θ we shall get one and only one point on the reference plane; conversely, for a given point on the plane r possesses a definite finite value but θ can have infinite number of value (viz ., θ, 2π + θ, 4π + θ,…….etc.).
(ii) The polar Co-ordinates of the pole are assumed to be (0, 0).
(iii) If the sense of radius vector is taken into account then the value of r may be negative. Thus, if the direction from O to P is taken as positive then the direction from P to O will be negative. Hence, if the points P, O, P’ are collinear such that OP = OP’ = r and ∠XOP = θ then the polar co-ordinates of P and P' are (r, θ) and (-r, θ) respectively.
However, in practice, it is convenient to take both the radius vector (r) and the vectorial angle (θ) as positive.
(iv) Remembering the rules regarding the signs of r and θ we can represent the polar co-ordinate of P in following different ways:
(r, θ); (-r, π + θ); [r, -(2π - θ)]; [-r, -(π - θ)].
● Co-ordinate Geometry
- What is Co-ordinate Geometry?
- Rectangular Cartesian Co-ordinates
- Polar Co-ordinates
- Relation between Cartesian and Polar Co-Ordinates
- Distance between Two given Points
- Distance between Two Points in Polar Co-ordinates
- Division of Line Segment: Internal & External
- Area of the Triangle Formed by Three co-ordinate Points
- Condition of Collinearity of Three Points
- Medians of a Triangle are Concurrent
- Apollonius' Theorem
- Quadrilateral form a Parallelogram
- Problems on Distance Between Two Points
- Area of a Triangle Given 3 Points
- Worksheet on Quadrants
- Worksheet on Rectangular – Polar Conversion
- Worksheet on Line-Segment Joining the Points
- Worksheet on Distance Between Two Points
- Worksheet on Distance Between the Polar Co-ordinates
- Worksheet on Finding Mid-Point
- Worksheet on Division of Line-Segment
- Worksheet on Centroid of a Triangle
- Worksheet on Area of Co-ordinate Triangle
- Worksheet on Collinear Triangle
- Worksheet on Area of Polygon
- Worksheet on Cartesian Triangle
From Polar Co-ordinates to HOME PAGE
Didn't find what you were looking for? Or want to know more information about Math Only Math. Use this Google Search to find what you need.
Recent Articles
-
Worksheet on Area of a Square and Rectangle | Area of Squares & Rectan
Jul 19, 25 05:00 AM
We will practice the questions given in the worksheet on area of a square and rectangle. We know the amount of surface that a plane figure covers is called its area. 1. Find the area of the square len… -
Area of Rectangle Square and Triangle | Formulas| Area of Plane Shapes
Jul 18, 25 10:38 AM
Area of a closed plane figure is the amount of surface enclosed within its boundary. Look at the given figures. The shaded region of each figure denotes its area. The standard unit, generally used for… -
What is Area in Maths? | Units to find Area | Conversion Table of Area
Jul 17, 25 01:06 AM
The amount of surface that a plane figure covers is called its area. It’s unit is square centimeters or square meters etc. A rectangle, a square, a triangle and a circle are all examples of closed pla… -
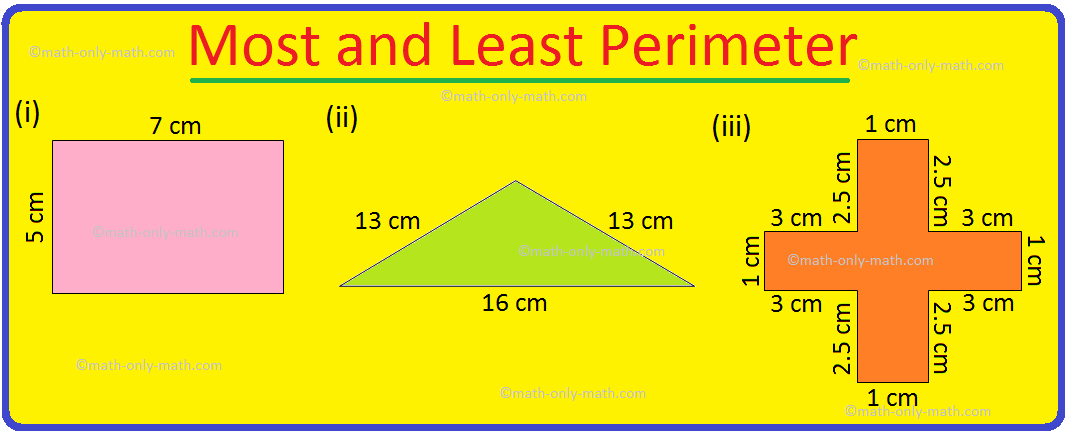
Worksheet on Perimeter | Perimeter of Squares and Rectangle | Answers
Jul 17, 25 12:40 AM
Practice the questions given in the worksheet on perimeter. The questions are based on finding the perimeter of the triangle, perimeter of the square, perimeter of rectangle and word problems. I. Find… -
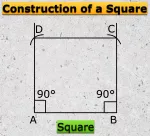
Formation of Square and Rectangle | Construction of Square & Rectangle
Jul 16, 25 11:46 PM
In formation of square and rectangle we will learn how to construct square and rectangle. Construction of a Square: We follow the method given below. Step I: We draw a line segment AB of the required…

New! Comments
Have your say about what you just read! Leave me a comment in the box below. Ask a Question or Answer a Question.