Magic Square
In a magic square, every row, column and each of the diagonals add up to the same total.
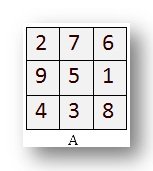
Here is a magic square. The numbers 1 to 9 are placed in the small
squares in such a way that no number is repeated and the sum of the
three digits column-wise, row-wise and diagonally is equal to 15.
This is a 3 by 3 magic square.
A. This is a magic square.
All 3 rows add upto 15.
All 3 columns add upto 15.
The 2 diagonals add upto 15.
There are 8 lines, each totaling 15.
In this magic square, numbers from 1 to 9 are used. In one of these lines, the numbers increase by 1.
The diagonal is 4, 5, 6.
Look carefully and find in which line does the numbers increase by (a) 2 (b) 3
Similar magic squares are also made.
There are the examples of magic squares formed by the numbers 5, 6, 7, 8, 9, 10, 11, 12 and 13 having the diagonally, row-wise and column-wise sum of 27
In the same pattern other magic squares may be formed.
(i) Numbers are 2, 3, 4, 5, 6, 7, 8, 9 and 10, Sum = 18
(ii) Numbers are 3 to 11 and sum = 21
(iii) Numbers are 4 to 12 and sum = 24
(iv) Numbers are 6 to 14 and sum = 30
(v) Numbers are 7 to 15 and sum = 33
(vi) Numbers are 8 to 16 and sum = 36
(vii) Numbers are 9 to 17 and sum = 39
Magic squares having 4 or more rows and columns may be made.
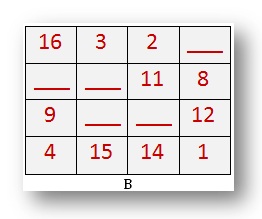
B. This is a 4 by 4 magic square. Find out the missing numbers. What does each line add up to?
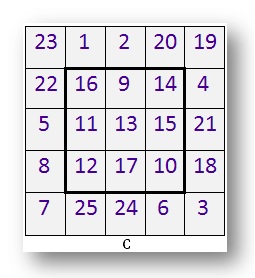
C. This is a 5 by 5 magic square.
It has 5 rows and 5 columns.
Find out the line total.
Check if each of the 5 rows, 5 columns and 2 diagonals add up to the same number.
At the centre of this 5 by 5 magic square is a 3 by 3 square. Draw this 3 by 3 square on a sheet of paper.
Copy the number in each box.
Is this 3 by 3 square A a magic square?
What is the line total of each row and column?
What is the total of the two diagonals? Do the numbers increase by 1 in any of the lines? Color that line.
Use different colors to shade lines where the numbers increase by (a) 2 (b) 3.
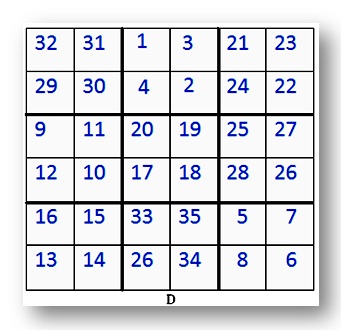
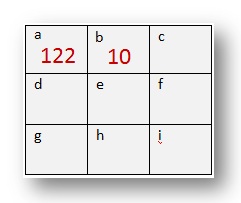
D. This is a 6 by 6 magic square.
Find the line total.
Check that some of the rows and columns add up to this number.
Notice that the thick lines divide the square into 9 smaller squares.
Each small square has 4 numbers.
What do you notice about the 4 numbers in each of this small square?
Add up the 4 numbers in each of the 9 squares.
Write your answer in a 3 by 3 square.
The first two squares haves been done for you.
(a) 29 + 30 + 31 + 32 = 122
(b) 1 + 2 + 3 + 4 = 10
(c) 21 + 22 +23 + 24 = ____
(d) 9 + 10 + 11 + 12 = ____
(e) 17 + 18 + 19 + 20 = ____
(f) 25 + 26 + 27 + 28 = ____
(g) 13 + 14 + 15 + 16 = ____
(h) 33 + 34 + 35 + 26 = ____
(i) 5 + 6 + 7 + 8 = ____
Now add up the numbers in each row, column, diagonal and confirm that this too is a magic square!
Observe the number pattern
1 ∙ 1 ∙ 2 ∙ 3 ∙ 5 ∙ 8 ∙ 13 ∙ 21 ∙ 34
Every number after the second number is equal to the sum of the two preceding numbers.
This type of relationship is called the Fibonacci sequence. It was developed by Leonardo Fibonacci of Italy around the year 1200.
We
can observe numbers from the Fibonacci sequence in various places in
nature; petals of flowers; leaves of plants; scales of pineapples and
nodes of a pine cone.
Observe the number pattern
1 ∙ 3 ∙ 6 ∙ 10 ∙ 15 ∙ 21
This number sequence is made up of triangular number.
The sequence begins with 1. Then
1 + 2 = 3
3 + 3 = 6
6 + 4 = 10
10 + 5 = 15
15 + 6 = 21
There is another interesting fact.
You can take a number of 3 digits as 356.
If we write after it the same number of three digits we get 356356.
This number is divided by 7, 11 and 13.
479479 is also divided by 7, 11 and 13.
Similarly, other numbers may be made which would be divisible by 7, 11 and 13.
Related Concept
● Patterns and Mental Mathematics
● Counting Numbers in Proper Pattern
● Puzzle
● Patterns
4th Grade Math Activities
From Magic Square to HOME PAGE
Didn't find what you were looking for? Or want to know more information about Math Only Math. Use this Google Search to find what you need.
Recent Articles
-
Perpendicular Lines | What are Perpendicular Lines in Geometry?|Symbol
Apr 19, 24 02:46 AM
In perpendicular lines when two intersecting lines a and b are said to be perpendicular to each other if one of the angles formed by them is a right angle. In other words, Set Square Set Square If two… -
Fundamental Geometrical Concepts | Point | Line | Properties of Lines
Apr 19, 24 01:55 AM
The fundamental geometrical concepts depend on three basic concepts — point, line and plane. The terms cannot be precisely defined. However, the meanings of these terms are explained through examples. -
What is a Polygon? | Simple Closed Curve | Triangle | Quadrilateral
Apr 18, 24 02:15 AM
What is a polygon? A simple closed curve made of three or more line-segments is called a polygon. A polygon has at least three line-segments. -
Simple Closed Curves | Types of Closed Curves | Collection of Curves
Apr 18, 24 01:36 AM
In simple closed curves the shapes are closed by line-segments or by a curved line. Triangle, quadrilateral, circle, etc., are examples of closed curves. -
Tangrams Math | Traditional Chinese Geometrical Puzzle | Triangles
Apr 18, 24 12:31 AM
Tangram is a traditional Chinese geometrical puzzle with 7 pieces (1 parallelogram, 1 square and 5 triangles) that can be arranged to match any particular design. In the given figure, it consists of o…