Fractions in Ascending Order

We will discuss here how to arrange the fractions in ascending order.

Solved examples for arranging in ascending order:

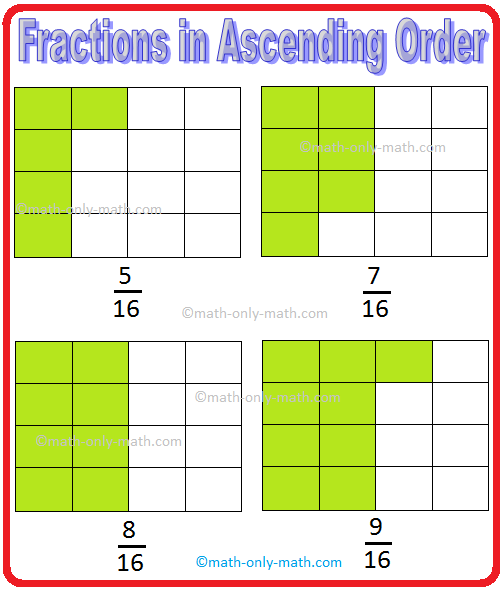
1. Let us arrange the fractions \(\frac{5}{16}\), \(\frac{9}{16}\), \(\frac{8}{16}\) and \(\frac{7}{16}\) in ascending order.

We know that above fractions are like fractions. We can arrange them in ascending order by comparing the numerators of each fraction. We can also compare these fractions by comparing the shaded parts in the given figures.

\(\frac{9}{16}\) > \(\frac{8}{16}\) > \(\frac{7}{16}\) > \(\frac{5}{16}\).

Hence, the ascending order is \(\frac{5}{16}\), \(\frac{7}{16}\), \(\frac{8}{16}\) and \(\frac{9}{16}\).

2. Arrange the following fractions 5/6, 8/9, 2/3 in ascending order.

First we find the L.C.M. of the denominators of the fractions to make the denominators same.

L.C.M. = 3 × 2 × 3 × 1 = 18

Now to make the fraction as like fractions divide the L.C.M. by the denominator of fractions, then multiply both the numerator and denominator of fraction with the number get after dividing L.C.M.

As in fraction 5/6 denominator is 6.

Divide 18 ÷ 6 = 3

Now, multiply both numerator and denominator by 3 = 5 × 3/6 × 3 = 15/18

Similarly, 8/9 = 8 × 2/9 × 2 = 16/18 (because 18 ÷ 9 = 2)

and 2/3 = 2 × 6/3 × 6 = 12/18 (because 18 ÷ 3 = 6)

Now, we compare the like fractions 15/18, 16/18 and 12/18

Comparing numerators, we find that 16 > 15 > 12

Therefore, 16/18 > 15/18 > 12/ 18

or, 8/9 > 5/6 > 2/3

or, 2/3 < 5/6 < 8/9

The ascending order of the fractions is 2/3, 5/6, 8/9.

3. Arrange the following fractions 1/2, 3/8, 2/3, 4/5 in ascending order.

First we find the L.C.M. of the denominators of the fractions to make the denominators same.

L.C.M. of 2, 8, 3 and 5 = 120

Now to make the fraction as like fractions divide the L.C.M. by the denominator of fractions, then multiply both the numerator and denominator of fraction with the number get after dividing L.C.M.

As in fraction 1/2 denominator is 2.

Divide 120 ÷ 2 = 60

Now, multiply both numerator and denominator by 60 = 1 × 60/2 × 60 = 60/120

Similarly, 3/8 = 3 × 15/8 × 15 = 45/120 (because 120 ÷ 8 = 15)

2/3 = 2 × 40/3 × 40 = 80/120 (because 120 ÷ 3 = 40)

and 4/5 = 4 × 24/5 × 24 = 96/120 (because 120 ÷ 5 = 24)

Now, we compare the like fractions 60/120, 45/120, 80/120 and 96/120

Comparing numerators, we find that 96 > 80 > 60 > 45

Therefore, 96/120 > 80/120 > 60/120 > 45/120

or 4/5 > 2/3 > 1/2 > 3/8

or 3/8 < 1/2 < 2/3 < 4/5

The ascending order of the fractions is 3/8 < 1/2 < 2/3 < 4/5.

4. Arrange the following fractions in ascending order of magnitude.

\(\frac{3}{4}\), \(\frac{5}{8}\), \(\frac{4}{6}\), \(\frac{2}{9}\) L.C.M. of 4, 8, 6 and 9 = 2 × 2 × 3 × 2 × 3 = 72

Ascending order: \(\frac{16}{72}\), \(\frac{45}{72}\), \(\frac{48}{72}\), \(\frac{54}{72}\)

                    i.e., \(\frac{2}{9}\), \(\frac{5}{8}\), \(\frac{4}{6}\), \(\frac{3}{4}\)   

5. Arrange the following fractions in ascending order of magnitude.

4\(\frac{1}{2}\), 3\(\frac{1}{2}\), 5\(\frac{1}{4}\), 1\(\frac{1}{6}\), 2\(\frac{1}{4}\)

Observe the whole numbers.

4, 3, 5, 1, 2

1 < 2 < 3 < 4 < 5

Therefore, ascending order: 1\(\frac{1}{6}\), 2\(\frac{1}{4}\), 3\(\frac{1}{2}\), 4\(\frac{1}{2}\), 5\(\frac{1}{4}\)

6. Arrange the following fractions in ascending order of magnitude.

3\(\frac{1}{4}\), 3\(\frac{1}{2}\), 2\(\frac{1}{6}\), 4\(\frac{1}{4}\), 8\(\frac{1}{9}\)

Observe the whole numbers.

3, 3, 2, 4, 8

Since the whole number part of 3\(\frac{1}{4}\) and 3\(\frac{1}{2}\) are same, compare them.

Which is bigger? 3\(\frac{1}{4}\) or 3\(\frac{1}{2}\)? \(\frac{1}{4}\) or \(\frac{1}{2}\)?

L.C.M. of 4, 2 = 4

\(\frac{1 × 1}{4 × 1}\) = \(\frac{1}{4}\)                 \(\frac{1 × 2}{2 × 2}\) = \(\frac{2}{4}\)

Therefore, 3\(\frac{1}{4}\) = 3\(\frac{1}{4}\)       3\(\frac{1}{2}\) = 3\(\frac{2}{4}\)

Therefore, 3\(\frac{2}{4}\) > 3\(\frac{1}{4}\)       i.e., 3\(\frac{1}{2}\) > 3\(\frac{1}{4}\)

Therefore, Ascending order: 2\(\frac{1}{6}\), 3\(\frac{1}{4}\), 3\(\frac{1}{2}\), 4\(\frac{3}{4}\), 8\(\frac{1}{9}\) 

Questions and Answers on Fractions in Ascending Order:

1. Arrange the given fractions in ascending order:

(i) \(\frac{13}{22}\), \(\frac{18}{22}\), \(\frac{10}{22}\), \(\frac{3}{22}\)

(ii) \(\frac{33}{42}\), \(\frac{16}{42}\), \(\frac{39}{42}\), \(\frac{9}{42}\)

Answers:

1. (i) \(\frac{3}{22}\), \(\frac{10}{22}\), \(\frac{13}{22}\), \(\frac{18}{22}\)

(ii) \(\frac{9}{42}\), \(\frac{16}{42}\), \(\frac{33}{42}\), \(\frac{39}{42}\)

2. Arrange the following fractions in ascending order of magnitude:

(i) \(\frac{7}{7}\), \(\frac{3}{7}\), \(\frac{1}{7}\), \(\frac{4}{7}\), \(\frac{2}{7}\), \(\frac{5}{7}\)

(ii) \(\frac{1}{2}\), \(\frac{3}{2}\), \(\frac{8}{3}\), \(\frac{4}{6}\), \(\frac{9}{2}\), \(\frac{1}{3}\)

Answer:

2. (i) \(\frac{1}{7}\), (\frac{2}{7}\), \(\frac{3}{7}\), \(\frac{4}{7}\), \(\frac{5}{7}\), \(\frac{7}{7}\)

(ii) \(\frac{1}{3}\), \(\frac{1}{2}\), \(\frac{4}{6}\), \(\frac{3}{2}\), \(\frac{8}{3}\), (\frac{9}{2}\)

Related Concept

● Fraction of a Whole Numbers

● Representation of a Fraction

● Equivalent Fractions

● Properties of Equivalent Fractions

● Like and Unlike Fractions

● Comparison of Like Fractions

● Comparison of Fractions having the same Numerator

● Types of Fractions

● Changing Fractions

● Conversion of Fractions into Fractions having Same Denominator

● Conversion of a Fraction into its Smallest and Simplest Form

● Addition of Fractions having the Same Denominator

● Subtraction of Fractions having the Same Denominator

● Addition and Subtraction of Fractions on the Fraction Number Line

4th Grade Math Activities

From Fractions in Ascending Order to HOME PAGE