Convert Exponentials and Logarithms
In convert Exponentials and Logarithms we will mainly discuss how to change the logarithm expression to Exponential expression and conversely from Exponential expression to logarithm expression.
To discus about convert Exponentials and Logarithms we need to first recall about logarithm and exponents.
The logarithm of any number to a given base is the index of the power to which the base must be raised in order to equal the given number. Thus, if aˣ = N, x is called the logarithm of N to the base a.
For example:
1. Since 3⁴ = 81, the logarithm of 81 to base 3 is 4.
2. Since 10¹ = 10, 10² = 100, 10³ = 1000, ………….
The natural number 1, 2, 3, …… are respectively the logarithms of 10, 100, 1000, …… to base 10.
The logarithm of N to base a is usually written as log₀ N, so that the same meaning is expressed by the two equations
ax = N; x = loga N
Examples on convert Exponentials and Logarithms
1. Convert the following exponential form to logarithmic form:(i) 104 = 10000
Solution:
104 = 10000
⇒ log10 10000 = 4
(ii) 3-5 = x
Solution:
3-5 = x
⇒ log3 x = -5
(iii) (0.3)3 = 0.027
Solution:
(0.3)3 = 0.027
⇒ log0.3 0.027 = 3
2. Convert the following logarithmic form to exponential form:
(i) log3 81 = 4
Solution:
log3 81 = 4
⇒ 34 = 81, which is the required exponential form.
(ii) log8 32 = 5/3
Solution:
log8 32 = 5/3
⇒ 85/3 = 32
(iii) log10 0.1 = -1
Solution:
log10 0.1 = -1
⇒ 10-1 = 0.1.
3. By converting to exponential form, find the values of following:
(i) log2 16
Solution:
Let log2 16 = x
⇒ 2x = 16
⇒ 2x = 24
⇒ x = 4,
Therefore, log2 16 = 4.
(ii) log3 (1/3)
Solution:
Let log3 (1/3) = x
⇒ 3x = 1/3
⇒ 3x = 3-1
⇒ x = -1,
Therefore, log3(1/3) = -1.
(iii) log5 0.008
Solution:
Let log5 0.008 = x
⇒ 5x = 0.008
⇒ 5x = 1/125
⇒ 5x = 5-3
⇒ x = -3,
Therefore, log5 0.008 = -3.
4. Solve the following for x:
(i) logx 243 = -5
Solution:
logx 243 = -5
⇒ x-5 = 243
⇒ x-5 = 35
⇒ x-5 = (1/3)-5
⇒ x = 1/3.
(ii) log√5 x = 4
Solution:
log√5 x = 4
⇒ x = (√5)4
⇒ x = (51/2)4
⇒ x = 52
⇒ x = 25.
(iii) log√x 8 = 6
Solution:
log√x 8 = 6
⇒ (√x)6 = 8
⇒ (x1/2)6 = 23
⇒ x3 = 23
⇒ x = 2.
Logarithmic Form Vs. Exponential Form
The logarithm function with base a has domain all positive real numbers and is defined byloga M = x ⇔ M = ax
● Write the exponential equation in logarithmic form.
24 = 16 ⇔ log2 16 = 4
10-2 = 0.01 ⇔ log10 0.01 = -2
81/3 = 2 ⇔ log8 2 = 1/3
6-1 = 1/6 ⇔ log6 1/6 = -1
● Write the logarithmic equation in exponential form.
● Solve for x:
1. log5 x = 2
x = 52
= 25
2. log81 x = ½
x = 811/2
⇒ x= (92)1/2
⇒ x = 9
3. log9 x = -1/2
x = 9-1/2
⇒ x = (32)-1/2
⇒ x = 3-1
⇒ x= 1/3
4. log7 x = 0
x= 70
⇒ x = 1
● Solve for n:
1. log3 27 = n
3n = 27
⇒ 3n = 33
⇒ n = 3
2. log10 10,000 = n
10n = 10,000
⇒ 10n = 104
⇒ n = 4
3. log49 1/7 = n
49n = 1/7
⇒ (72)n = 7-1
⇒ 72n = 7-1
⇒ 2n = -1
⇒ n = -1/2
4. log36 216 = n
36n = 216
⇒ (62)n = 63
⇒ 62n= 63
⇒ 2n = 3
⇒ n = 3/2
● Solve for b:
1. logb 27 = 3
b3 = 27
⇒ b3 = 33
⇒ b = 3
2. logb 4 = 1/2
b1/2 = 4
⇒ (b1/2)2 = 42
⇒ b = 16
3. logb 8 = -3
b-3 = 8 ⇒ b-3 = 23
⇒ (b-1)3 = 23
⇒b-1 = 2
⇒ 1/b = 2
⇒ b = ½
4. logb 49 = 2
b2 = 49
⇒ b2 = 72
⇒ b = 7
● If f(x) = log3 x, find f(1).
Solution:
f(1) = log3 1 = 0 (since logarithm of 1 to any finite non-zero base is zero.)
Therefore f(1) = 0
● A number that is domain of the function y = log10 x is
(a) 1
(b) 0
(c) ½
(d) =10
Answer: (b)
● The graph of y = log4 x lines entirely in quadrants
(a) I and II
(b) II and III
(c) I and III
(d) I and IV
● At what point does the graph of y = log5 x intersect the x-axis?
(a) (1, 0)
(b) (0, 1)
(c) (5, 0)
(d) There is no point of intersection.
Answer: (a)
● Mathematics Logarithm
Convert Exponentials and Logarithms
Common Logarithm and Natural Logarithm
Logarithms
11 and 12 Grade Math
From Convert Exponentials and Logarithms to HOME PAGE
Didn't find what you were looking for? Or want to know more information about Math Only Math. Use this Google Search to find what you need.
Recent Articles
-
Symmetrical Shapes | One, Two, Three, Four & Many-line Symmetry
Apr 23, 24 04:50 PM
Symmetrical shapes are discussed here in this topic. Any object or shape which can be cut in two equal halves in such a way that both the parts are exactly the same is called symmetrical. The line whi… -
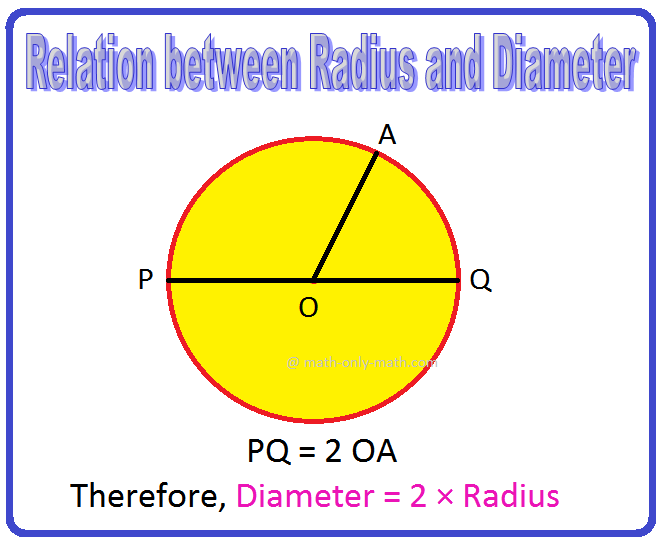
Relation between Diameter Radius and Circumference |Problems |Examples
Apr 23, 24 03:15 PM
Relation between diameter radius and circumference are discussed here. Relation between Diameter and Radius: What is the relation between diameter and radius? Solution: Diameter of a circle is twice -
Circle Math | Terms Related to the Circle | Symbol of Circle O | Math
Apr 22, 24 01:35 PM
In circle math the terms related to the circle are discussed here. A circle is such a closed curve whose every point is equidistant from a fixed point called its centre. The symbol of circle is O. We… -
Preschool Math Activities | Colorful Preschool Worksheets | Lesson
Apr 21, 24 10:57 AM
Preschool math activities are designed to help the preschoolers to recognize the numbers and the beginning of counting. We believe that young children learn through play and from engaging -
Months of the Year | List of 12 Months of the Year |Jan, Feb, Mar, Apr
Apr 20, 24 05:39 PM
There are 12 months in a year. The months are January, February, march, April, May, June, July, August, September, October, November and December. The year begins with the January month. December is t…