Conversion from
Circular to Sexagesimal System
Worked-out problems on the conversion from circular to sexagesimal system:
1. In a right-angled triangle the difference between two acute angles is 2π/5. Express these two angles in terms of radian and degree.
Solution:
Let the acute angles be xc and yc. (According to the condition of the problem:x + y = π/2 and x - y = 2π/5
Solving these two equations we get;
x = 1/2 (π/2 + 2π/5)
x = 1/2 (5π + 4π/10)
x = 1/2 (9π/10)
x = 9π/20
and y = 1/2 (π/2 - 2π/5)
y = 1/2 (5π - 4π/10)
y = 1/2 (π/10)
y = π/20
Again, x = (9 × 180°)/20 = 81°
y = 180°/20 = 9°
2. The circular measure of an angle is π/8; find its value in sexagesimal systems.
Solution:
πc/8We know, πc = 180°
πc/8 = 180°/8
πc/8 = 22.5° = 22° + 0.5°
[Now we will convert 0.5° to minute.
0.5° = (0.5 × 60)’ ; since 1° = 60’
= 30’]
πc/8 = 22° 30’
Therefore, the sexagesimal measures of the angle π/8 is 22° 30’
The above solved problems help us to learn in trigonometry, about the conversion from circular to sexagesimal system.
Basic Trigonometry
Measurement of Trigonometric Angles
Relation between Sexagesimal and Circular
Conversion from Sexagesimal to Circular System
Conversion from Circular to Sexagesimal System
From Conversion from Circular to Sexagesimal System to Home Page
Didn't find what you were looking for? Or want to know more information about Math Only Math. Use this Google Search to find what you need.
Recent Articles
-
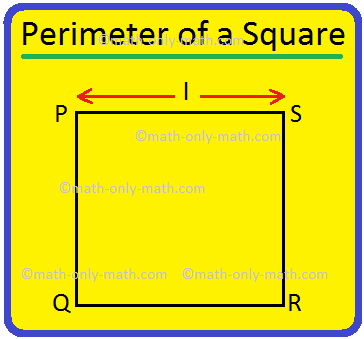
Perimeter of a Square | How to Find the Perimeter of Square? |Examples
Apr 25, 24 05:34 PM
We will discuss here how to find the perimeter of a square. Perimeter of a square is the total length (distance) of the boundary of a square. We know that all the sides of a square are equal. Perimete… -
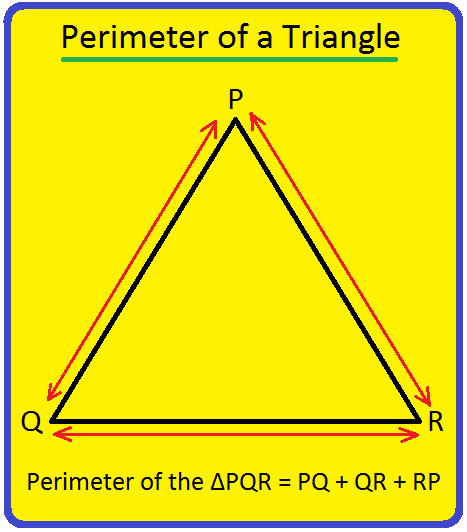
Perimeter of a Triangle | Perimeter of a Triangle Formula | Examples
Apr 25, 24 05:13 PM
We will discuss here how to find the perimeter of a triangle. We know perimeter of a triangle is the total length (distance) of the boundary of a triangle. Perimeter of a triangle is the sum of length… -
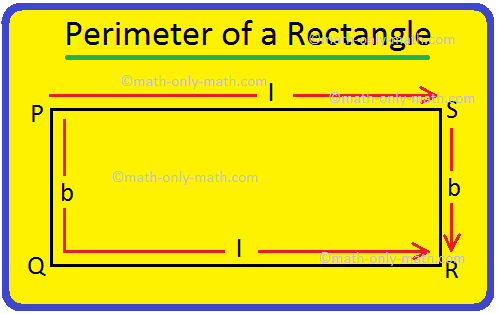
Perimeter of a Rectangle | How to Find the Perimeter of a Rectangle?
Apr 25, 24 03:45 PM
We will discuss here how to find the perimeter of a rectangle. We know perimeter of a rectangle is the total length (distance) of the boundary of a rectangle. ABCD is a rectangle. We know that the opp… -
Dividing 3-Digit by 1-Digit Number | Long Division |Worksheet Answer
Apr 24, 24 03:46 PM
Dividing 3-Digit by 1-Digit Numbers are discussed here step-by-step. How to divide 3-digit numbers by single-digit numbers? Let us follow the examples to learn to divide 3-digit number by one-digit nu… -
Symmetrical Shapes | One, Two, Three, Four & Many-line Symmetry
Apr 24, 24 03:45 PM
Symmetrical shapes are discussed here in this topic. Any object or shape which can be cut in two equal halves in such a way that both the parts are exactly the same is called symmetrical. The line whi…