Construct Different Types of Quadrilaterals

How to construct different types of quadrilaterals?

The different types of quadrilaterals are constructed and classified by relationships of their sides, angles and diagonals. 

Some of the constructions of different types of quadrilaterals are given below along with the steps-by-step explanation.

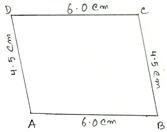
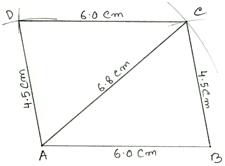
1. Construct a parallelogram ABCD in which AB = 6 cm, BC = 4.5 cm and diagonal AC = 6.8 cm.

Solution:

Draw a rough sketch of the required parallelogram and write down the given dimensions. (Rough Sketch) →

Steps of Construction:

(i) Draw AB = 6 cm.

(ii) With A as center and radius 6.8 cm, draw an arc.

(iii) With B as center and radius 4.5 cm draw another arc, cutting the previous arc at C.

(iv) Join BC and AC.

(v) With A as center and radius 4.5 cm, draw an arc.

(vi) With C as center and radius 6 cm draw another arc, cutting the previously drawn arc at D.

(vii) Join DA and DC.

Then, ABCD is the required parallelogram.

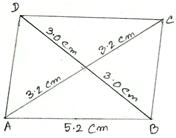
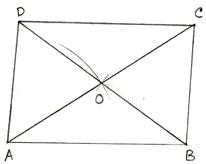
2. Construct a parallelogram, one of whose sides is 5.2 cm and whose diagonals are 6 cm and 6.4 cm.

Solution:

We know that the diagonals of a parallelogram bisect each other.
Make a rough sketch of the required parallelogram, as shown. (Rough Sketch) →

Steps of Construction:

(i) Draw AB = 5.2 cm.

(ii) With A as center and radius 3.2 cm, draw an arc.

(iii) With B as center and radius 3 cm draw another arc, cutting the previous arc at O.

(iv) Join OA and OB.

(v) Produce AO to C such that OC = AO and produce BO to D such that OD = OB.

(vi) Join AD, BC and CD.

Then, ABCD is the required parallelogram.

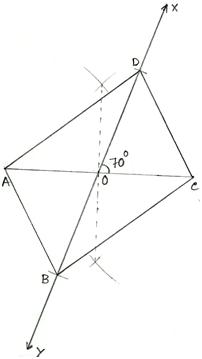
3. Construct a parallelogram whose diagonals are 5.4 cm and 6.2 cm and an angle between them is 70°. 

Solution:

We know that the diagonals of a parallelogram bisect each other.
So, we may proceed according to the steps given below.

Steps of Construction:

(i) Draw AC = 5.4 cm.

(ii) Bisect AC at O.

(iii) Make ∠COX = 70° and produce XO to Y.

(iv) Set off OB = 1/2 (6.2) = 3.1 cm and OD = 1/2 (6.2) =3.1 cm as shown.

(v) Join AB, BC, CD and DA.


Then, ABCD is the required parallelogram.

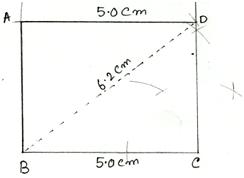
4. Construct a rectangle ABCD in which side BC = 5 cm and diagonal BD = 6.2 cm.

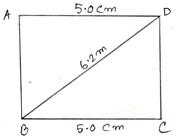
Solution:

First draw a rough sketch of the required rectangle and write down its dimensions.

Now, we may construct it by following the steps given below. (Rough Sketch) →

Steps of Construction:

(i) Draw BC = 5 cm.

(ii) Draw CX ⊥ BC.

(iii) With B as center and radius 6.2 cm draw an arc, cutting CX at D.

(iv) Join BD.

(v) With D as center and radius 5 cm, draw an arc.

(vi) With B as center and radius equal to CD draw another arc, cutting the previous arc at A.

(vii) Join AB and AD.

Then, ABCD is the required rectangle.

5. Construct a square ABCD, each of whose diagonals is 5.2 cm.

Solution:

We know that the diagonals of a square bisect each other at right angles.

So, we proceed according to the following steps.

Steps of Construction:

(i) Draw AC = 5.2 cm. (ii) Draw the right bisector XY of AC, meeting AC at O.

(iii) From O set off OB = 1/2 (5.2) = 2.6 cm along OY and OD = 2.6 cm along OX.

(iv) Join AB, BC, CD and DA.

Then, ABCD is the required square.



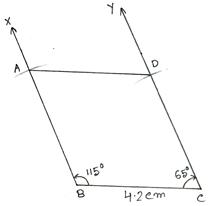
6. Construct a rhombus with side 4.2 cm and one of its angles equal to 65°.

Solution:

Clearly, the adjacent angle = (180° - 65°) = 115°. So, we may proceed according to the steps given below.

Steps of Construction:

(i) Draw BC = 4.2 cm.

(ii) Make ∠CBX = 115° and ∠BCY = 65°.

(iii) Set off BA = 4.2 cm along BX and CD = 4.2 cm along CY.

(iv) Join AD.

Then, ABCD is the required rhombus.


To construct different types of quadrilaterals students can follow the explanation given in the steps of the construction of quadrilateral.

● Related Concepts on Quadrilateral

● What is Quadrilateral?

● Different Types of Quadrilaterals

● Construction of Quadrilaterals

● Construct Different Types of Quadrilaterals

● Quadrilateral - Worksheets

● Quadrilateral Worksheet

● Worksheet on Construction on Quadrilateral

● Worksheet on Different Types of Quadrilaterals

8th Grade Math Practice

From Construct Different Types of Quadrilaterals to HOME PAGE