Subscribe to our ▶️YouTube channel🔴 for the latest videos, updates, and tips.
Home | About Us | Contact Us | Privacy | Math Blog
Comparison of Ratios
In comparison of ratios, we first need to convert them into like fractions by using the following steps and then compare them.
Step I: Obtain the given ratios.
Step II: Now we express each of the given ratios as a fraction in the simplest form.
Step III: Find the L.C.M (least common multiple) of the denominators of the fractions obtained in the above step (Step II).
Step IV: Obtain the first fraction and its denominator. Divide the L.C.M (least common multiple) obtained in the above step (Step III) by the denominator to get a number z (say).
Now, multiply the numerator and denominator of the fraction by the z (L.C.M). Similarly apply the same procedure to the all other fraction.
In other words convert each fraction to its equivalent fractions with denominator equal to the L.C.M (least common multiple).
Thus, the denominators of all the fractions are be same.
Step V: Compare the numerators of the equivalent fractions
whose denominators are same.
Compare the numerators of the fractions obtained in the above step (Step IV). The fraction having larger numerator will be larger than the other fraction.
Two or more ratios can be compared by writing their equivalent fractions with common denominators.
Solved examples of comparison of ratios:
1. Compare the ratios 4 : 5 and 2 : 3.
Solution:
Express the given ratios as fraction
4 : 5 = 4/5 and 2 : 3 =2/3
Now find the L.C.M (least common multiple) of 5 and 3
The L.C.M (least common multiple) of 5 and 3 is 15.
Making the denominator of each fraction equal to 15, we have
4/5 = (4 ×3)/(5 ×3) = 12/15 and 2/3 = (2 ×5)/(3 ×5) = 10/15
Clearly, 12 > 10
Now, 12/15 > 10/15
Therefore, 4 : 5 > 2 : 3.
2. Compare the ratios 5 : 6 and 7 : 9.
Solution:
Express the given ratios as fraction
5 : 6 = 5/6 and 7 : 9 =7/9
Now find the L.C.M (least common multiple) of 6 and 9
The L.C.M (least common multiple) of 6 and 9 is 18.
Making the denominator of each fraction equal to 18, we have
5/6 = (5 ×3)/(6 ×3) = 15/18 and 7/9 = (7 ×2)/(9 ×2) = 14/18
Clearly, 15 > 14
Now, 15/18 > 14/18
Therefore, 5 : 6 > 7 : 9.
3. Compare the ratios 1.2 : 2.5 and 3.5 : 7.
Solution:
1.2 : 2.5 = 1.2/2.5 and 3.5 : 7 =3.5/7
1.2/2.5 = (1.2 ×10)/(2.5 ×10 ) = 12/25 and 3.5/7 = (3.5 ×10)/(7 ×10) = 35/70 = 1/2
[We removed the decimal point from the ratios now, we will compare the ratio]
Now find the L.C.M (least common multiple) of 25 and 2
The L.C.M (least common multiple) of 25 and 2 is 50.
Making the denominator of each fraction equal to 50, we have
= 12/25 = (12 ×2)/(25 ×2) = 24/50 and 1/2 = (1 ×25)/(2 ×25) = 25/50
Now, 25/50 > 24/50
Therefore, 3.5 : 7 > 1.2 : 2.5.
6th Grade Page
From Comparison of Ratios to HOME PAGE
Didn't find what you were looking for? Or want to know more information about Math Only Math. Use this Google Search to find what you need.
Recent Articles
-
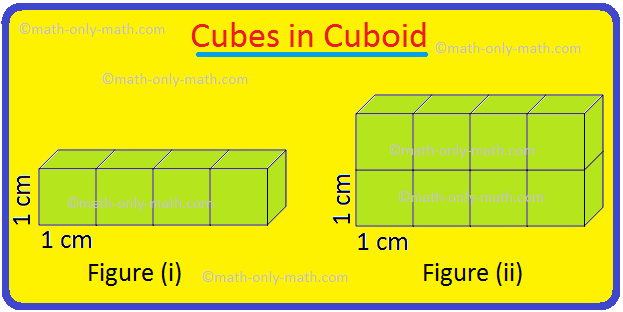
Volume of a Cuboid | Volume of Cuboid Formula | How to Find the Volume
Jul 20, 25 12:39 PM
Cuboid is a solid box whose every surface is a rectangle of same area or different areas. A cuboid will have a length, breadth and height. Hence we can conclude that volume is 3 dimensional. To measur… -
5th Grade Volume | Units of Volume | Measurement of Volume|Cubic Units
Jul 20, 25 10:22 AM
Volume is the amount of space enclosed by an object or shape, how much 3-dimensional space (length, height, and width) it occupies. A flat shape like triangle, square and rectangle occupies surface on… -
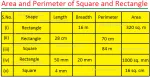
Worksheet on Area of a Square and Rectangle | Area of Squares & Rectan
Jul 19, 25 05:00 AM
We will practice the questions given in the worksheet on area of a square and rectangle. We know the amount of surface that a plane figure covers is called its area. 1. Find the area of the square len… -
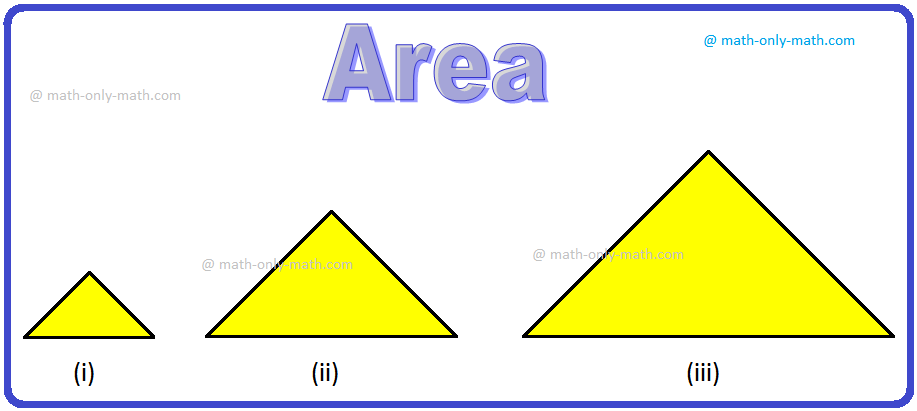
Area of Rectangle Square and Triangle | Formulas| Area of Plane Shapes
Jul 18, 25 10:38 AM
Area of a closed plane figure is the amount of surface enclosed within its boundary. Look at the given figures. The shaded region of each figure denotes its area. The standard unit, generally used for… -
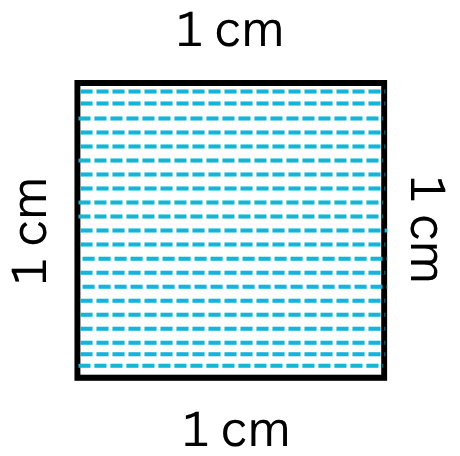
What is Area in Maths? | Units to find Area | Conversion Table of Area
Jul 17, 25 01:06 AM
The amount of surface that a plane figure covers is called its area. It’s unit is square centimeters or square meters etc. A rectangle, a square, a triangle and a circle are all examples of closed pla…


New! Comments
Have your say about what you just read! Leave me a comment in the box below. Ask a Question or Answer a Question.