Circle Touches y-axis

We will learn how to find the equation of a circle touches y-axis.

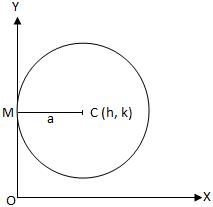
The equation of a circle with centre at (h, k) and radius equal to a, is (x - h)\(^{2}\) + (y - k)\(^{2}\) = a\(^{2}\).

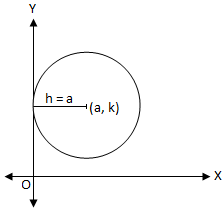
When the circle touches y-axis i.e., h = a.

Then the equation (x - h)\(^{2}\) + (y - k)\(^{2}\) = a\(^{2}\) becomes  (x - a)\(^{2}\) + (y - k)\(^{2}\) = a\(^{2}\)

If a circle touches the y-axis, then the x-co-ordinate of the centre will be equal to the radius of the circle. 

Hence, the equation of the circle will be of the form (x - a)\(^{2}\) + (y - k)\(^{2}\) = a\(^{2}\)

Circle Touches y-axisCircle Touches y-axis
Circle Touches the y-axisCircle Touches the y-axis

Let C (h, k) be the centre of the circle. Since the circle touches the y-axis, therefore, a = h

Hence the equation of the circle is (x - a)\(^{2}\) + (y - k)\(^{2}\) = a\(^{2}\) ⇒ x\(^{2}\) + y\(^{2}\) – 2ax – 2ky + k\(^{2}\) = 0

 

Solved examples on the central form of the equation of a circle touches y-axis:

1. Find the equation of a circle whose y-coordinate of the centre is -7 and radius is 3 units also touches the y-axis.

Solution:

The required equation of the circle whose y-coordinate of the centre is -7 and radius is 3 units also touches the y-axis is (x - 3)\(^{2}\) + (y + 7)\(^{2}\) = 3\(^{2}\), [Since radius is equal to the x-coordinate of the centre]

⇒ x\(^{2}\) – 6x + 9 + y\(^{2}\) + 14y + 49 = 9

⇒ x\(^{2}\) + y\(^{2}\) - 6x  + 14y + 49 = 0


2. Find the equation of a circle whose radius is 9 units and y-coordinate of the centre is -6 and also touches the y-axis.

Solution:

The required equation of the circle whose radius is 9 units and y-coordinate of the centre is -6 and also touches the x-axis is (x - 9)\(^{2}\) + (y + 6)\(^{2}\) = 9\(^{2}\), [Since radius is equal to the x-coordinate of the centre]

⇒ x\(^{2}\) - 18x + 81 + y\(^{2}\) + 12y + 36 = 81

⇒ x\(^{2}\) + y\(^{2}\) - 18x + 12y + 36 = 0

● The Circle




11 and 12 Grade Math 

From Circle Touches y-axis to HOME PAGE




Didn't find what you were looking for? Or want to know more information about Math Only Math. Use this Google Search to find what you need.



Share this page: What’s this?

Recent Articles

RSS

  1. What is a Polygon? | Simple Closed Curve | Triangle | Quadrilateral

    Apr 19, 24 01:22 PM

    Square - Polygon
    What is a polygon? A simple closed curve made of three or more line-segments is called a polygon. A polygon has at least three line-segments.

    Read More

  2. Perpendicular Lines | What are Perpendicular Lines in Geometry?|Symbol

    Apr 19, 24 02:46 AM

    Perpendicular Lines
    In perpendicular lines when two intersecting lines a and b are said to be perpendicular to each other if one of the angles formed by them is a right angle. In other words, Set Square Set Square If two…

    Read More

  3. Fundamental Geometrical Concepts | Point | Line | Properties of Lines

    Apr 19, 24 01:55 AM

    Point P
    The fundamental geometrical concepts depend on three basic concepts — point, line and plane. The terms cannot be precisely defined. However, the meanings of these terms are explained through examples.

    Read More

  4. Simple Closed Curves | Types of Closed Curves | Collection of Curves

    Apr 18, 24 01:36 AM

    Closed Curves Examples
    In simple closed curves the shapes are closed by line-segments or by a curved line. Triangle, quadrilateral, circle, etc., are examples of closed curves.

    Read More

  5. Tangrams Math | Traditional Chinese Geometrical Puzzle | Triangles

    Apr 18, 24 12:31 AM

    Tangrams
    Tangram is a traditional Chinese geometrical puzzle with 7 pieces (1 parallelogram, 1 square and 5 triangles) that can be arranged to match any particular design. In the given figure, it consists of o…

    Read More