arccot(x) - arccot(y) = arccot(\(\frac{xy + 1}{y - x}\))
We will learn how to prove the property of the inverse trigonometric function arccot(x) - arccot(y) = arccot(\(\frac{xy + 1}{y - x}\)) (i.e., cot\(^{-1}\) x + cot\(^{-1}\) y = cot\(^{-1}\) (\(\frac{xy + y}{y - x}\))
Proof:
Let, cot\(^{-1}\) x = α and cot\(^{-1}\) y = β
From cot\(^{-1}\) x = α we get,
x = cot α
and from cot\(^{-1}\) y = β we get,
y = cot β
Now, cot (α - β) = (\(\frac{cot α cot β + 1}{cot β - tan α}\))
cot (α - β) = \(\frac{xy + 1}{y - x}\)
⇒ α - β = cot\(^{-1}\) \(\frac{xy + 1}{y - x}\)
⇒ cot\(^{-1}\) x - cot\(^{-1}\) y = cot\(^{-1}\) \(\frac{xy + 1}{y - x}\)
Therefore, cot\(^{-1}\) x - cot\(^{-1}\) y = cot\(^{-1}\) \(\frac{xy + 1}{y - x}\)
● Inverse Trigonometric Functions
- General and Principal Values of sin\(^{-1}\) x
- General and Principal Values of cos\(^{-1}\) x
- General and Principal Values of tan\(^{-1}\) x
- General and Principal Values of csc\(^{-1}\) x
- General and Principal Values of sec\(^{-1}\) x
- General and Principal Values of cot\(^{-1}\) x
- Principal Values of Inverse Trigonometric Functions
- General Values of Inverse Trigonometric Functions
- arcsin(x) + arccos(x) = \(\frac{π}{2}\)
- arctan(x) + arccot(x) = \(\frac{π}{2}\)
- arctan(x) + arctan(y) = arctan(\(\frac{x + y}{1 - xy}\))
- arctan(x) - arctan(y) = arctan(\(\frac{x - y}{1 + xy}\))
- arctan(x) + arctan(y) + arctan(z)= arctan\(\frac{x + y + z – xyz}{1 – xy – yz – zx}\)
- arccot(x) + arccot(y) = arccot(\(\frac{xy - 1}{y + x}\))
- arccot(x) - arccot(y) = arccot(\(\frac{xy + 1}{y - x}\))
- arcsin(x) + arcsin(y) = arcsin(x \(\sqrt{1 - y^{2}}\) + y\(\sqrt{1 - x^{2}}\))
- arcsin (x) - arcsin(y) = arcsin (x \(\sqrt{1 - y^{2}}\) - y\(\sqrt{1 - x^{2}}\))
- arccos (x) + arccos(y) = arccos(xy - \(\sqrt{1 - x^{2}}\)\(\sqrt{1 - y^{2}}\))
- arccos(x) - arccos(y) = arccos(xy + \(\sqrt{1 - x^{2}}\)\(\sqrt{1 - y^{2}}\))
- 2 arcsin(x) = arcsin(2x\(\sqrt{1 - x^{2}}\))
- 2 arccos(x) = arccos(2x\(^{2}\) - 1)
- 2 arctan(x) = arctan(\(\frac{2x}{1 - x^{2}}\)) = arcsin(\(\frac{2x}{1 + x^{2}}\)) = arccos(\(\frac{1 - x^{2}}{1 + x^{2}}\))
- 3 arcsin(x) = arcsin(3x - 4x\(^{3}\))
- 3 arccos(x) = arccos(4x\(^{3}\) - 3x)
- 3 arctan(x) = arctan(\(\frac{3x - x^{3}}{1 - 3 x^{2}}\))
- Inverse Trigonometric Function Formula
- Principal Values of Inverse Trigonometric Functions
- Problems on Inverse Trigonometric Function
11 and 12 Grade Math
From arccot(x) - arccot(y) to HOME PAGE
Didn't find what you were looking for? Or want to know more information about Math Only Math. Use this Google Search to find what you need.
Recent Articles
-
Fundamental Geometrical Concepts | Point | Line | Properties of Lines
Apr 18, 24 02:58 AM
The fundamental geometrical concepts depend on three basic concepts — point, line and plane. The terms cannot be precisely defined. However, the meanings of these terms are explained through examples. -
What is a Polygon? | Simple Closed Curve | Triangle | Quadrilateral
Apr 18, 24 02:15 AM
What is a polygon? A simple closed curve made of three or more line-segments is called a polygon. A polygon has at least three line-segments. -
Simple Closed Curves | Types of Closed Curves | Collection of Curves
Apr 18, 24 01:36 AM
In simple closed curves the shapes are closed by line-segments or by a curved line. Triangle, quadrilateral, circle, etc., are examples of closed curves. -
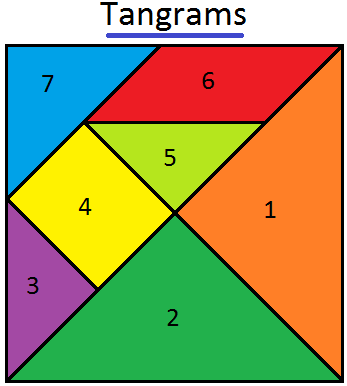
Tangrams Math | Traditional Chinese Geometrical Puzzle | Triangles
Apr 18, 24 12:31 AM
Tangram is a traditional Chinese geometrical puzzle with 7 pieces (1 parallelogram, 1 square and 5 triangles) that can be arranged to match any particular design. In the given figure, it consists of o… -
Time Duration |How to Calculate the Time Duration (in Hours & Minutes)
Apr 17, 24 01:32 PM
We will learn how to calculate the time duration in minutes and in hours. Time Duration (in minutes) Ron and Clara play badminton every evening. Yesterday, their game started at 5 : 15 p.m.