Unlike Terms
The unlike terms not having the same literal coefficients.
For example:
(i) 5ab, 5a, 5ac are unlike terms because they do not have identical variables.
(iii) 2x, 2y, 2m are unlike terms.
Now look at the terms of the following polynomials:
(i) 11a2b2 + 3ab2We observe that two terms of the binomial (11a2b2 and 3ab2) have same variables raised to different powers. So, the binomial is made up of two unlike terms or dissimilar terms.
(ii) 7m2 - 2m + 10m3
We observe that the three terms of the trinomial have same variables (m) raised to different
powers. So, the above trinomial is made up of three unlike or dissimilar terms.
We observe that the three terms of the trinomial (3x2, 5xy and 7x2y) have different variables raised to different powers. So, the trinomial is made up of three unlike terms.
(iv) 11m3n3 - nm + 9m2 - 4m2n2
We observe that the four terms of the polynomials (11m3n3, nm, 9m2 and 4m2n2) have different variables raised to different power. The numerical coefficients are also different. So, the polynomials is made up of four unlike or dissimilar terms.
Examples to identify unlike or dissimilar terms:
Identify which pairs contain unlike terms in the following:
(i) 5ab, 7ab
(ii) 3x, 4x2(iii) m, n
(iv) 2m2, 3m3
(v) 6a2b, 11ab2
(vi) –xy, 7yx
Solution:
(i) 5ab, 7ab
The terms 5ab and 7ab have same literal factors (ab) so this pair is a like term.
The terms 3x and 4x2 have different literal factors so this pair is an unlike term.
(iii) m, n
The terms m and n have different literal factors so this pair is an unlike term.
The terms 2m2 and 3m3 have different literal factors so this pair is an unlike term.
(v) 6a2b, 11ab2
The terms 6a^2b and 11ab^2 have different literal factors so this pair is an unlike term.
(vi) –xy, 7yx
The terms –xy and 7yx have same literal factors (xy) so this pair is a like term.
● Terms
Adding and Subtracting Like Terms
Algebra Page
6th Grade Page
From Unlike Terms to HOME PAGE
Didn't find what you were looking for? Or want to know more information about Math Only Math. Use this Google Search to find what you need.
Recent Articles
-
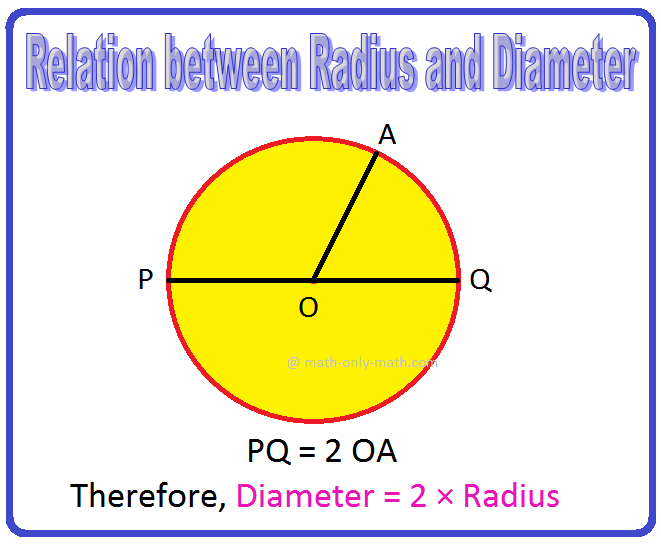
Relation between Diameter Radius and Circumference |Problems |Examples
Apr 22, 24 05:19 PM
Relation between diameter radius and circumference are discussed here. Relation between Diameter and Radius: What is the relation between diameter and radius? Solution: Diameter of a circle is twice -
Circle Math | Terms Related to the Circle | Symbol of Circle O | Math
Apr 22, 24 01:35 PM
In circle math the terms related to the circle are discussed here. A circle is such a closed curve whose every point is equidistant from a fixed point called its centre. The symbol of circle is O. We… -
Preschool Math Activities | Colorful Preschool Worksheets | Lesson
Apr 21, 24 10:57 AM
Preschool math activities are designed to help the preschoolers to recognize the numbers and the beginning of counting. We believe that young children learn through play and from engaging -
Months of the Year | List of 12 Months of the Year |Jan, Feb, Mar, Apr
Apr 20, 24 05:39 PM
There are 12 months in a year. The months are January, February, march, April, May, June, July, August, September, October, November and December. The year begins with the January month. December is t… -
What are Parallel Lines in Geometry? | Two Parallel Lines | Examples
Apr 20, 24 05:29 PM
In parallel lines when two lines do not intersect each other at any point even if they are extended to infinity. What are parallel lines in geometry? Two lines which do not intersect each other
● Terms - Worksheets
Worksheet on Like and Unlike Terms
Worksheet on Addition of Like Terms
Worksheet on Subtraction of Like Terms
Worksheet on Adding and Subtracting Like Terms
Worksheet on Combining Like Terms
Worksheet on Addition of Unlike Terms