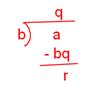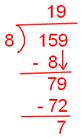Properties of Division
The properties of division of whole numbers are as follows :
Property 1:
If a and b (b not equal to zero) are whole numbers, then a ÷ b (expressed as a/b) is not necessarily a whole number.
In other words, whole numbers are not closed for division.
Verification: We know that dividing a whole number a by a non-zero whole number b means finding a whole numbers c such that a = bc.
Consider the division of 14 by 3. We find that there is no whole number which when multiplied by 3 gives us 14. So, 14 ÷ 3 is not a whole number. Similarly, 12, 5, 9, 4, 37, 6 etc. are not whole numbers.
Property 2:
If a is any whole number, then a ÷ 1 = a.
In other words, any whole number divided by 1 gives the quotient as the number itself.
Division by 1:
When any number is divided by 1, we always get the number itself as the quotient.
For Example:
645 ÷ 1 = 645 7895 ÷ 1 = 7895 85692 ÷ 1 = 85692
Verification: We know that
(i) 1 × 5 = 5
Therefore, 5 ÷ 1 = 5
(ii) 1 × 11 = 11
Therefore, 11 ÷ 1 = 11
(iii) 1 × 29 = 29
Therefore, 29 ÷ 1 = 29
(iv) 1 × 116 = 116
Therefore, 116 ÷ 1 = 116
(v) 1 × 101 = 101
Therefore, 101 ÷ 1 = 101
(vi) 1 × 1 = 1
Therefore, 1 ÷ 1 = 1
Property 3:
If a is any whole number other than zero, then a ÷ a = 1.
In other words, any whole number (other than zero) divided by itself gives 1 as the quotient.
Division by itself:
When any number is divided by the number itself, we always get 1 as the quotient.
For Example:
567 ÷ 567 = 1 5478 ÷ 5478 = 1 24768 ÷ 24768 = 1
Verification: We have,
(i) 13 = 13 × 1
Therefore, 13 ÷ 13 = 1
(ii) 9 = 9 × 1
Therefore, 9 ÷ 9 = 1
(iii) 17 = 17 × 1
Therefore, 17 ÷ 17 = 1
(iv) 123 = 123 × 1
Therefore, 123 ÷ 123 = 1
(v) 21 = 21 × 1
Therefore, 21 ÷ 21 = 1
(vi) 1 = 1 × 1
Therefore, 1 ÷ 1 = 1
Property 4:
Zero divided by any whole number (other than zero) gives the quotient as zero. In other words, if a is a whole numbers other than zero, then 0 ÷ a = 0
Division of 0 by any number:
When 0 is divided by any number, we always get 0 as the quotient.
For Example:
0 ÷ 953 = 0 0 ÷ 5759 = 0 0 ÷ 46357 = 0
Verification : We have,
(i) 0 × 7 = 0
Therefore, 0 ÷ 7 = 0
(ii) 0 × 11 = 0
Therefore, 0 ÷ 11 = 0
(iii) 0 × 17 = 0
Therefore, 0 ÷ 17 = 0
(iv) 0 × 132 = 0
Therefore, 0 ÷ 132 = 0
(v) 0 × 164 = 0
Therefore, 0 ÷ 164 = 0
Note:
In order to divide 6 by 0, we must find a whole number which when multiplied by 0 gives us 6. Clearly, no such number can be obtained. We, therefore, say that division by 0 is not defined.
Property 5:
Let a, b and c is the whole numbers and b ≠ 0, c ≠ 0. If a ÷ b = c, then b × c = a.
Verification: We have,
(i) 15 ÷ 3 = 5
Therefore, 5 × 3 = 15
(ii) 27 ÷ 9 = 3
Therefore, 9 × 3 = 27
(iii) 56 ÷ 7 = 8
Therefore, 7 × 8 = 56
(iv) 99 ÷ 11 = 9
Therefore, 11 × 9 = 99
(i) 75 ÷ 15 = 5
Therefore, 15 × 5 = 75
Property 6:
Let a, b and c be whole numbers and b ≠ 0, c ≠ 0. If b × c = a, then a ÷ c = b and a ÷ b = c.
Verification: We have,
(i) 18 = 3 × 6
Therefore, 16 ÷ 3 = 8 and 16 ÷ 8 = 3
(ii) 42 = 6 × 7
Therefore, 42 ÷ 6 = 7 and 42 ÷ 7 = 6
(iii) 72 = 8 × 9
Therefore, 72 ÷ 9 = 8 and 72 ÷ 8 = 9
(iv) 48 = 8 × 6
Therefore, 48 ÷ 6 = 8 and 48 ÷ 8 = 6
(v) 24 = 12 × 2
Therefore, 24 ÷ 2 = 12 and 24 ÷ 12 = 2
Property 7:
(Division Algorithm) If a whole number a is divided by a non-zero whole number b, then there exists whole numbers q and r such that a = bq + r, where either r = 0 or, r < b.
This can also be expressed as:
Related to this we have the following definitions:
DIVIDEND: The number which is to be divided is called dividend.In this case, a is the dividend.
DIVISOR: Divisor is the number by which the dividend is divided.Here, b is the divisor.
QUOTIENT: The number of times the divisor divides the dividend is called the quotient.
Here, q is the quotient.
REMAINDER: The number which is left over after division is called the remainder.
Here, r is the remainder. Clearly r = a – bq
Using these terms, the division algorithm can be restated as:
Dividend = Divisor × Quotient + Remainder.
Verification: Let a = 159 and b = 8.
By actual division, we find that
Quotient (q) = 19
And, Remainder (r) = 7
Clearly, 159 = 19 × 8 + 7 i.e. a = bq + r.
Note: The divisor can never be zero. Division by zero is not possible.
Representation of Whole Numbers on Number Line
Division as The Inverse of Multiplication
Numbers Page
6th Grade Page
From Properties of Division to HOME PAGE
Didn't find what you were looking for? Or want to know more information about Math Only Math. Use this Google Search to find what you need.
Recent Articles
-
2nd Grade Geometry Worksheet | Plane and Solid Shapes | Point | Line
Dec 10, 24 02:35 PM
2nd grade geometry worksheet -
Types of Lines |Straight Lines|Curved Lines|Horizontal Lines| Vertical
Dec 09, 24 10:39 PM
What are the different types of lines? There are two different kinds of lines. (i) Straight line and (ii) Curved line. There are three different types of straight lines. (i) Horizontal lines, (ii) Ver… -
Points and Line Segment | Two Points in a Curved Surface | Curve Line
Dec 09, 24 01:08 AM
We will discuss here about points and line segment. We know when two lines meet we get a point. When two points on a plane surface are joined, a straight line segment is obtained. -
Solid Shapes | Basic Geometric Shapes | Common Solid Figures | Plane
Dec 08, 24 11:19 PM
We will discuss about basic solid shapes. We see a variety of solid objects in our surroundings. Solid objects have one or more shapes like the following. Match the objects with similar shape. -
2nd grade math Worksheets | Free Math Worksheets | By Grade and Topic
Dec 07, 24 03:38 PM
2nd grade math worksheets is carefully planned and thoughtfully presented on mathematics for the students.
New! Comments
Have your say about what you just read! Leave me a comment in the box below. Ask a Question or Answer a Question.