<title>Apr 16, Math Place Value | Place Value | Place Value Chart | Ones and Tens</title>
<link>https://www.math-only-math.com/math-place-value.html</link>
<guid isPermaLink="false">300541cd3cd64c05d358ed4c80684056</guid>
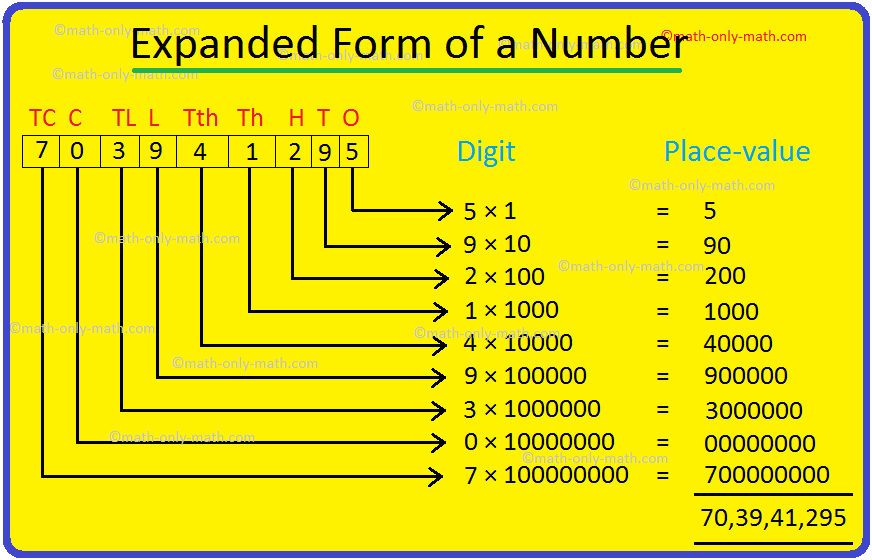
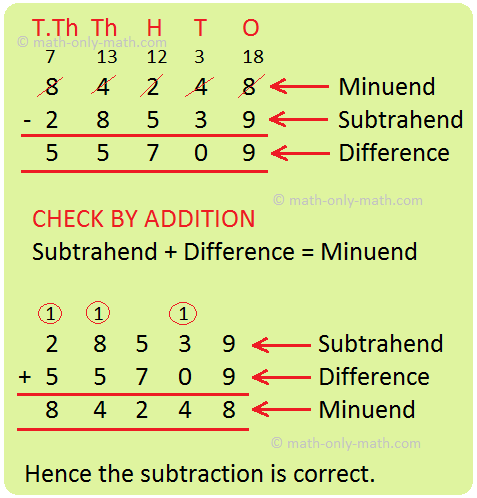
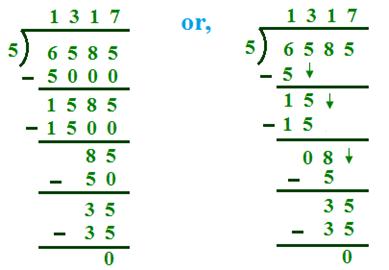
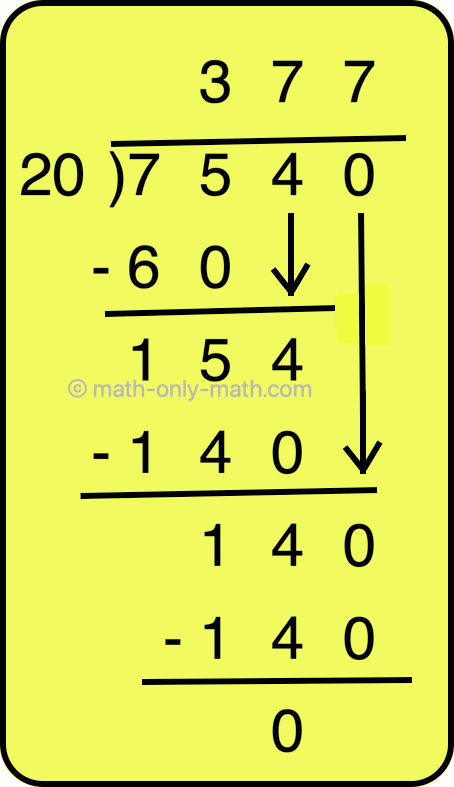
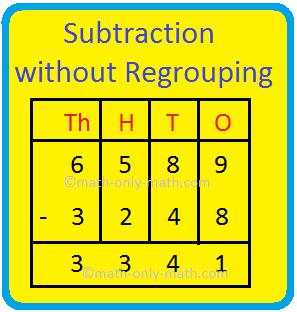
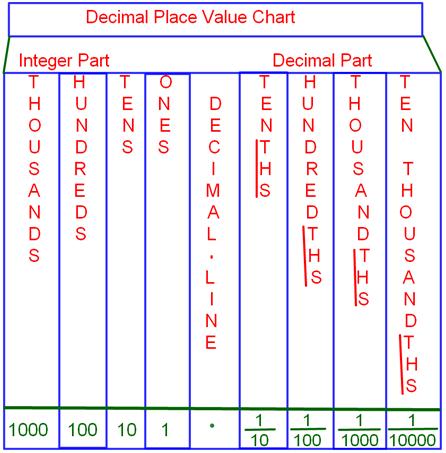
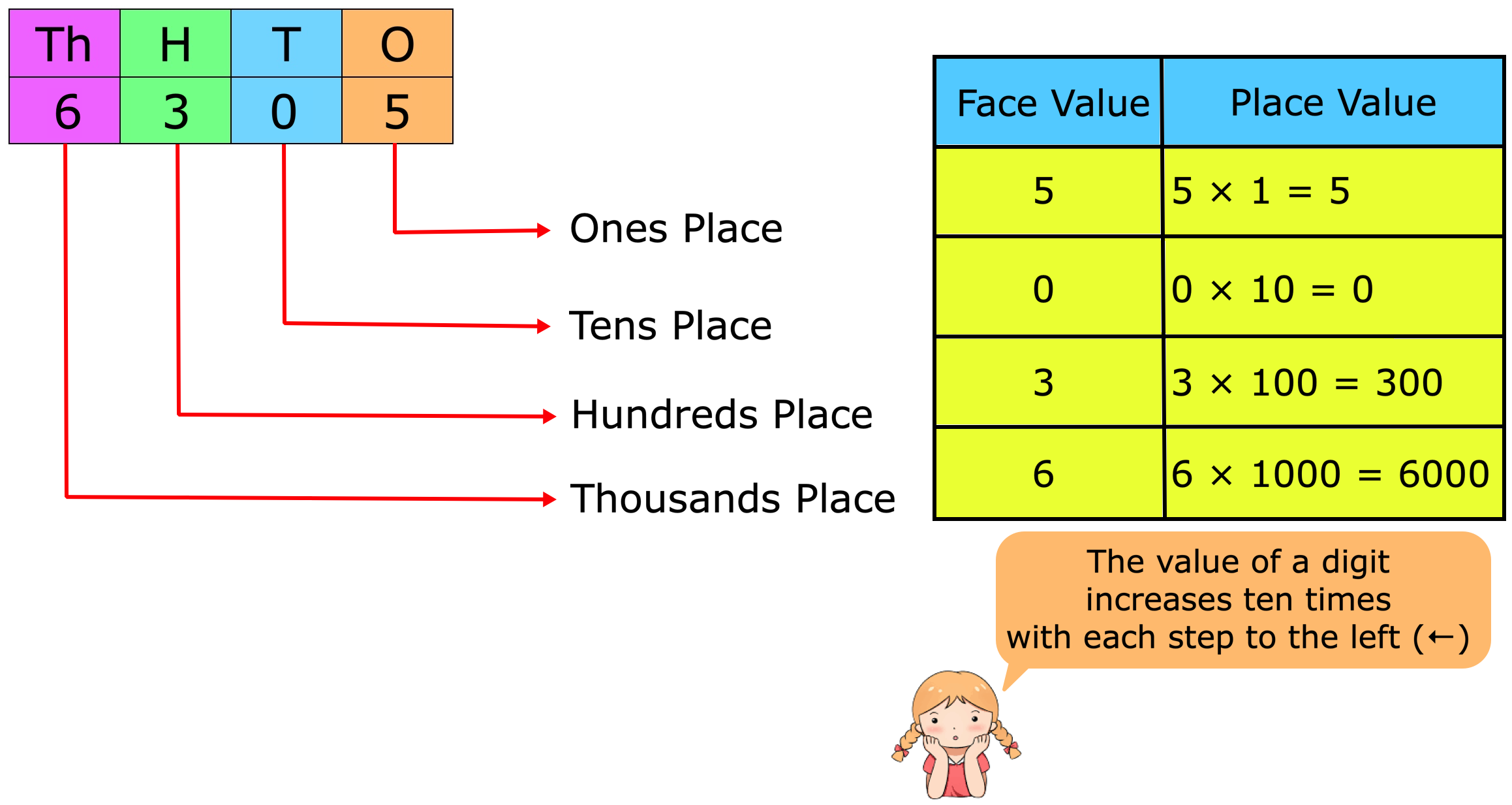
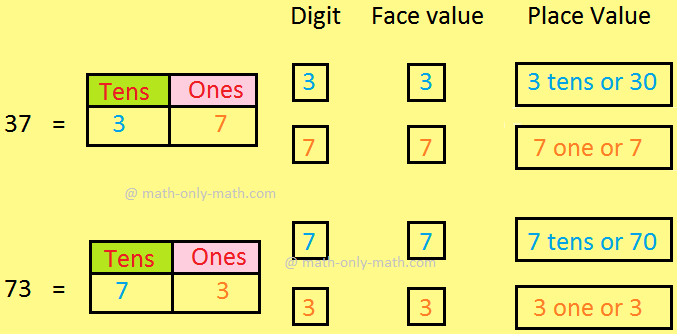
<description>0, 1, 2, 3, 4, 5, 6, 7, 8 and 9 are one-digit numbers. Numbers from 10 to 99 are two-digit numbers. Let us look at the digit 6 in the number 64. It is in the tens place of the number. 6 tens = 60 So, the place value of 6 is 60.</description>
<pubDate>Wed, 16 Apr 2025 15:10:27 -0400</pubDate>